Sistema de mallas. Circuitos eléctricos
Sistema de mallas
Ejemplo n° 1
Determinar las incógnitas de todo el circuito.
Desarrollo
Datos:
V1 = 20 V
V2 = 30 V
V3 = 10 V
V4 = 20 V
Rpar = 10 Ω
Rimpar = 5 Ω
Esquema:
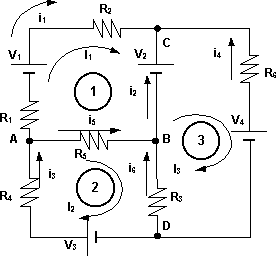
Esquema del circuito para resolver por el método de mallas
Solución
(1) V1- V2 = I1·(R1 + R2 + R5) - I2·R5 - I3·0
(2) V3 = I2·(R4 + R5 + R3) - I1·R5 - I3·R3
(3) V2- V4 = -I1·0 - I2·R3 + I3·(R3 + R6)
Reemplazando:
(1) 20 V - 30 V = I1·(10 Ω + 5 Ω + 10 Ω) - I2·10 Ω - I3·0
(2) 10 V = I2·(5 Ω + 10 Ω + 10 Ω) - I1·10 Ω - I3·10 Ω
(3) 30 V - 20 V = -I1·0 - I2·10 Ω + I3·(10 Ω + 5 Ω)
(1) -10 V = I1·25 Ω - I2·10 Ω - I3·0
(2) 10 V = -I1·10 Ω + I2·25 Ω - I3·10 Ω
(3) 10 V = -I1·0 - I2·10 Ω + I3·15 Ω
1) Determinante de todas las incógnitas = Δ
| Δ = | 25 Ω -10 Ω 0 Ω | -10 Ω 25 Ω -10 Ω | 0 Ω -10 Ω 15 Ω |
Δ = (9.375 + 0 + 0) Ω³ - (0 + 1.500 + 2.500) Ω³
Δ = 5.375 Ω³
2) Determinante de I1 = Δ1
| Δ1 = | -10 V 10 V 10 V | -10 Ω 25 Ω -10 Ω | 0 Ω -10 Ω 15 Ω |
Δ1 = (-3.750 + 1.000 + 0) V·Ω² - (0 - 1.000 - 1.500) V·Ω²
Δ1 = -250 V·Ω²
3) Determinante de I2 = Δ2
| Δ2 = | 25 Ω -10 Ω 0 Ω | -10 V 10 V 10 V | 0 Ω -10 Ω 15 Ω |
Δ2 = (3.750 + 0 + 0) V·Ω² - (0 - 2.500 + 1.500) V·Ω²
Δ2 = 4.750 V·Ω²
4) Determinante de I3 = Δ3
| Δ3 = | 25 Ω -10 Ω 0 Ω | -10 Ω 25 Ω -10 Ω | -10 V 10 V 10 V |
Δ3 = (6.250 - 1.000 + 0) V·Ω² - (0 + 1.000 - 2.500) V·Ω²
Δ3 = 6.750 V·Ω²
Luego:
| I1 = | Δ1 |
| Δ |
| I1 = | -250 V·Ω² |
| 5.375 Ω³ |
I1 = -0,047 A
| I2 = | Δ2 |
| Δ |
| I2 = | 4.750 V·Ω² |
| 5.375 Ω³ |
I2 = 0,884 A
| I3 = | Δ3 |
| Δ |
| I3 = | 6.750 V·Ω² |
| 5.375 Ω³ |
I3 = 1,256 A
A I1 se le invierte el sentido por ser negativo.
i1 = I1 = 0,047 A
i3 = I2 = 0,884 A
i4 = I3 = 1,256 A
i6 = I3 - I2 = 0,372 A
i5 = I1 + I2 = 0,931 A
i2 = I3 + I1 = 1,303 A
Para verificar se pueden aplicar las leyes de Kirchhoff
1) Se estudia una malla (1° ley)
2) Se estudia un nodo (2° ley)
Otro método consiste en comparar la potencia de los elementos activos contra la potencia de los elementos pasivos.
P2 = V2·I2 = 30 V·1,303 A = 39,09 W
P3 = V3·I3 = 10 V·0,884 A = 8,84 W
P4 = V4·I4 = 20 V·1,256 A = 25,12 W
P1 = V1·I1 = 20 V·0,047 A = 0,94 W
Potencia de elementos activos = 47,93 W
PR12 = (R2 + R1)·i1² = 15 Ω·(0,047 A)² = 0,0331 W
PR4 = R4·i3² = 5 Ω·(0,884 A)² = 3,9073 W
PR6 = R6·i4² = 5 Ω·(1,256 A)² = 7,8877 W
PR5 = R5·i5² = 10 Ω·(0,931 A)² = 8,6676 W
PR3 = R3·i6² = 10 Ω·(0,372 A)² = 1,3838 W
Potencia de elementos pasivos = 47,94 W
| Potencia de elementos activos Potencia de elementos pasivos | = 47,93 W = -47,94 W |
| ≈0 W |
Medición de tensiones en corriente contínua
También se puede medir corriente alterna mediante rectificación previa.
Bobina móvil/imán permanente
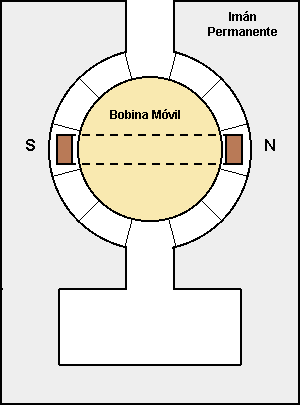
Esquema básico para medir tensión
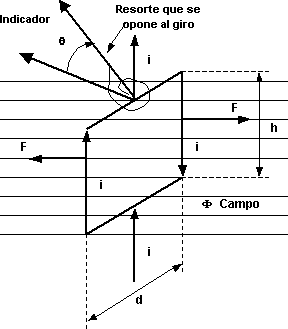
Diagrama del circuito, el campo eléctrico, las fuerzas y los momentos
CM = F·d
CM: cupla motríz
F: fuerza (N)
d: ancho de la espira.
Pero: F = Φ·h·i
CM = Φ·d·h·i
CM = k·i (1)
CR = θ·U (2)
CR: cupla del resorte
θ: ángulo
U: constante del resorte (en física I era k, ver apunte "Fuerza elástica")
En el equilibrio debe ser:
CM = CR
k·i = θ·U
| θ = | k·i |
| U |
Comercialmente se obtienen instrumentos con las siguientes características:
Resistencia de la bobina: RB = 2 a 20 Ω
Corriente máxima en la bobina: iM = 0,1 a 10 mA
Para el amperímetro:
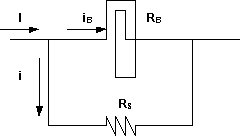
Esquema básico para medir corriente
iB·RB = i·RS
I = iB + i
i = I - iB
iB·RB = (I - iB)·RS
iB·RB = I·RS - iB·RS
iB·RB + iB·RS = I·RS
iB·(RB + RS) = I·RS
| I | = | RB + RS |
| iB | RS |
| I | = m |
| iB |
m: Poder de multiplicación shunt
RB + RS = m·RS
RB = RS·(m - 1)
| RS = | RB |
| m - 1 |
Ejemplo n° 2
Para:
I1 = 1 A
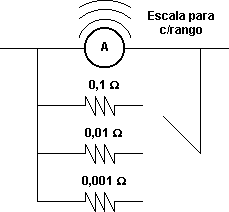
Diagrama de un circuito para medir corriente
| m1 = | 1 A |
| 0,01 A |
m1 = 100
| RS1 = | 10 Ω |
| 100 - 1 |
| RS1 = | 10 Ω |
| 99 |
RS1 = 0,1 Ω
Ejemplo n° 3
Para calcular 2 rangos más:
I2 = 10 A
I3 = 100 A
| m2 = | 10 A |
| 0,01 A |
m2 = 1.000
| RS2 = | 10 Ω |
| 1.000 - 1 |
| RS2 = | 10 Ω |
| 999 |
RS2 = 0,01 Ω
| m3 = | 100 A |
| 0,01 A |
m3 = 10.000
| RS3 = | 10 Ω |
| 10.000 - 1 |
| RS3 = | 10 Ω |
| 9.999 |
RS3 = 0,001 Ω
Las resistencias internas equivalentes del amperímetro es muy muy muy pequeña.
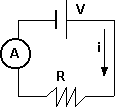
Diagrama de un circuito para medir corriente
El amperímetro se conecta en serie.
Para el voltímetro:
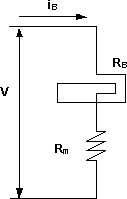
Esquema básico para medir tensión
V = (RB + Rm)·iB
| iB = | VB |
| RB |
| V = | (RB + Rm)·VB |
| RB |
| m = | V |
| VB |
m: poder multiplicador shunt
| m = | RB + Rm |
| RB |
RB + Rm = m·RB
Rm = RB·(m - 1)
Ejemplo n° 4
Para calcular un voltímetro de 4 rangos:
V1 = 100 V
V2 = 200 V
V3 = 500 V
V4 = 1.000 V
| m1 = | 100 V |
| 0,1 V |
m1 = 1.000
Rm1 = 10 Ω·(1.000 - 1)
Rm1 = 10 Ω·999
Rm1 = 9.990 Ω
| m2 = | 200 V |
| 0,1 V |
m2 = 2.000
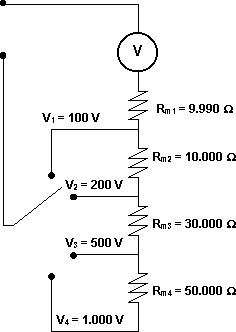
Diagrama de un circuito para medir tensión
Rm2 = 10 Ω·(2.000 - 1) - Rm1
Rm2 = 10 Ω·1.999 - 9.990 Ω
Rm2 = 19.999 Ω - 9.990 Ω
Rm2 = 10.000 Ω
| m3 = | 500 V |
| 0,1 V |
m3 = 5.000
Rm3 = 10 Ω·(5.000 - 1) - Rm1 - Rm2
Rm3 = 10 Ω·4.999 - 10.000 Ω - 9.990 Ω
Rm3 = 49.990 Ω - 19.990 Ω
Rm3 = 30.000 Ω
| m4 = | 1.000 V |
| 0,1 V |
m4 = 10.000
Rm4 = 10 Ω·(10.000 - 1) - Rm1 - Rm2 - Rm3
Rm4 = 10 Ω·9.999 - 10.000 Ω - 9.990 Ω - 30.000 Ω
Rm4 = 99.990 Ω - 49.990 Ω
Rm4 = 50.000 Ω
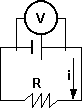
Diagrama de un circuito para medir tensión
Las resistencias internas equivalentes del voltímetro son muy grandes. El voltímetro se conecta en paralelo.
Autor: Ricardo Santiago Netto. Argentina
¿Qué es una corriente de malla?