Ejemplo n° 1 de estática
Ejemplo n° 1
Si:
F1 = 200 N, en el eje X dirigida hacia la derecha.
F2 = 300 N, 60° por encima del eje X, hacia la derecha.
F3 = 100 N, 45° sobre el eje X, hacia la derecha.
F4 = 200 N, en la dirección negativa del eje Y.
Encontrar la fuerza resultante.
Solución
Graficamos las fuerzas y luego proyectamos las componentes sobre los ejes:
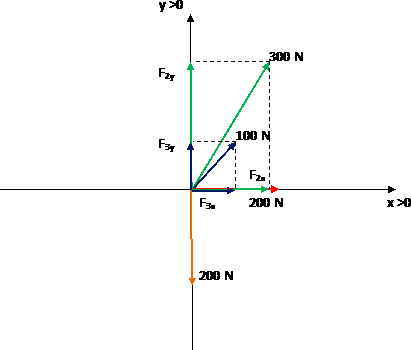
Lugo sumamos las componentes sobre cada eje:
En X:
F1 + F2x + F3x = FTx (fuerza total en x)
En Y:
F2y + F3y - F4 = FTy (fuerza total en y)
Para hallar el valor de cada componente utilizamos trigonometría, coseno y seno.
| cos 60° = | F2x |
| 300 N |
F2x = 300 N·cos 60° ⇒ F2x = 300 N·0,5 ⇒ F2x = 150 N
| cos 45° = | F3x |
| 100 N |
F3x = 100 N·cos 45° ⇒ F3x = 100 N·0,71 ⇒ F3x = 70,71 N
| sen 60° = | F2y |
| 300 N |
F2y = 300 N·sen 60° ⇒ F2y = 300 N·0,87 ⇒ F2y = 259,81 N
| sen 45° = | F3y |
| 100 N |
F3y = 100 N·sen 45° ⇒ F3y = 100 N·0,71 ⇒ F3y = 70,71 N
Finalmente armamos las ecuaciones y hacemos las cuentas:
En X:
200 N + 150 N + 70,71 N = FTx ⇒ FTx = 420,71 N
En Y:
259,81 N + 70,71 N - 200 N = FTy ⇒ FTy = 130,52 N
Ya tenemos las componentes de la fuerza resultante:
FTx = 420,71 N
FTy = 130,52 N
Ahora hay que hallar el módulo de la fuerza compuesta mediante el teorema de Pitágoras:
FT² = FTx² + FTy² ⇒ FT² = (420,71 N)² + (130,52 N)²
FT² = 17.035,4704 N² + 176.996,9041 N² ⇒ FT² = 194.032,3745 N² ⇒ FT = 440,49 N
Nuevamente con la trigonometría hallamos el ángulo, siendo α el ángulo entre la fuerza y el eje X:
| tg α = | FTy |
| FTx |
| artg | FTy | = α |
| FTx |
| α = arctg | 130,52 N |
| 420,71 N |
α = arctg 0,31 ⇒ α = 17,24°
Resultado, el módulo de la fuerza resultante es:
FT = 440,49 N
Resultado, el á de la fuerza resultante es:
α = 17,24°
Autor: Ricardo Santiago Netto. Argentina
Ejemplo, cómo calcular la fuerza resultante