Propiedades de las funciones derivables
LEMA (de monotonía)
Sea x: I ⟶ ℜ una función. Supongamos que f'(t0) > 0 en un punto t0 interior. Entonces existe Δ > 0 tal que f(s) < f(t0) < f(t) cuando s ∈ (t0 - Δ, t0) y t ∈ (t0, t0 + Δ), es decir, es creciente en t0
Análogamente si f'(t0) < 0, es decreciente en t0
Teorema de Rolle
Sea x:[a, b] ⟶ ℜ una función contínua en [a, b] y derivable en (a, b). Si f(a) = f(b) entonces existe c ε (a, b) tal que f'(c) = 0.
Teorema de Cauchy
Sean f:[a, b] ⟶ ℜ y g:[a, b] ⟶ ℜ continuas en [a, b] y derivables en (a, b). Entonces existe c ∈ (a, b) tal que:
[f(b) - f(a)]·g'(c) = [g(b) - g(a)]·f'(c).
Teorema del valor medio (o de los incrementos finitos)
Sea x:[a, b] ⟶ ℜ una función contínua en [a, b] y derivable en (a, b). Entonces existe c ε (a, b) tal que f(b) - f(a) = (b - a)·f'(c).
Consecuencias del teorema del valor medio
1) Teorema del valor medio sobre monotonía
▫ Sea x:[a, b] ⟶ ℜ una función contínua en [a, b] y derivable en (a, b). Entonces:
- Si f'(t) ≥ 0 para todo t ε (a, b) entonces f es monótona creciente en [a, b]
- Si f'(t) ≤ 0 para todo t ε (a, b) entonces f es monótona decreciente en [a, b]
- Si f'(t) = 0 para todo t ε (a, b) entonces f es constante en [a, b]
2) Si f y g son funciones continuas en [a, b] y derivables en (a, b) tales que f'(x) = g'(x) para todo x ∈ (a, b), entonces existe un número real c tal que f(x) = g(x) + c para todo x ∈ [a, b]; es decir, las dos funciones f y g se diferencian en una constante.
Estudio local de una función
Crecimiento y decrecimiento de una función
Definición:
Sea x:[a, b] ⟶ ℜ, x0 ∈ (a, b), se dice que f es creciente en x0 si existe un entorno de x0, E(x0, h) tal que:
| Si x0 - h < x < x0 | ⟶ | f(x) < f(x0) |
| Si x0 < x < x0 + h | ⟶ | f(x0) < f(x) |
Se dice que f es decreciente si (-f) es creciente.
• Proposición 1 "monotonía":
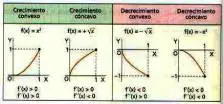
Crecimiento y decrecimiento de una función
Sea x:(a, b) ⟶ ℜ una función derivable y x0 ∈ (a, b). Entonces:
Si f'(x0) > 0, f es creciente en x0
Si f'(x0) < 0, f es decreciente en x0
Observación:
La condición es suficiente pero no es necesaria. Ejemplo: f(x) = x³
• Proposición 2:
Sea x:(a, b) ⟶ ℜ una función, x0 ∈ (a, b), f derivable en x0 y creciente (decreciente). Entonces f'(x0) ≥ 0 (f'(x0) ≤ 0).
Máximos y mínimos relativos
Condiciones para la determinación de extremos
Definición:
Sea f:[a, b] ⟶ ℜ, x0 ∈ (a, b), se dice que f tiene un máximo/mínimo relativo en, x0 si existe un entorno de x0, E(x0, h) tal que ∀ x ∈ E(x0, h) se tiene que f(x) ≤ f(x0)/f(x) ≥ f(x0).
Condición necesaria
f derivable en x0 ∈ (a, b) y presenta en x0 un máximo o mínimo, entonces f'(x0) = 0.
Condición suficiente
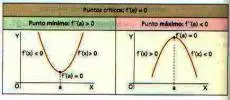
Máximo y mínimo de una función
• Proposición 1:
Sea x:[a, b] ⟶ ℜ contínua en I, x0 ∈ (a, b) y f derivable en el intervalo (x0-Δ, x0 + Δ) contenido en I salvo quizás x0
a)
Si f'(x) > 0, x ∈ (x0 - Δ, x0) (f creciente a la izquierda de x0)
f'(x) < 0, x ∈ (x0, x0 + Δ) (f decreciente a la derecha de x0)
Entonces f presente un máximo relativo en x0
b)
Análogamente para mínimo relativo.
• Proposición 2:
f:[a, b] ⟶ ℜ, x0 ∈ (a, b) tal que f'(x0) = 0 y f"(x0) ≠ 0.
Entonces:
f"(x0) > 0 entonces x0 es mínimo relativo.
f"(x0) < 0 entonces x0 es máximo relativo.
Condición necesaria y suficiente
Sea x:[a, b] ⟶ ℜ contínua en [a, b], x0 ∈ (a, b) tal que f'(x0) = 0.
Supongamos que f admite derivadas sucesivas (finitas) en un intervalo centrado en x0 y supongamos que la primera derivada que no se anula en x0 es fn(x0), derivada n-ésima de f.
En estas condiciones:
"la condición necesaria y suficiente para que f presente en x0 un máximo o mínimo relativo es que n sea par. Además si fn (x0) < 0 ( > 0) será un máximo (mínimo) relativo".
Además si n es impar existe un punto de inflexión de tangente horizontal.
Concavidad y convexidad
Definición:
Función cóncava: Una función f es cóncava en el punto x0 cuando la tangente a la gráfica de f en el punto (x0, f(x0)) queda por debajo de la gráfica de la función.
De otra manera: Una función se dice cóncava hacia arriba si la recta que une dos puntos de la gráfica queda por encima de la gráfica.
Función convexa: Una función f es convexa en el punto x0 cuando la tangente a la gráfica de f en el punto (x0, f(x0)) queda por encima de la gráfica de la función.
De otra manera: Una función se dice cóncava hacia abajo si la recta que une dos puntos de la gráfica queda por debajo de la gráfica.
Condición suficiente de concavidad
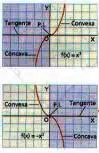
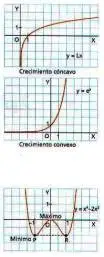
Si una función f es tal que ∀ x ∈ (a, b) f"(x) > 0 entonces f es cóncava hacia arriba en (a, b)
Si una función f es tal que ∀ x ∈ (a, b) f"(x) < 0 entonces f es cóncava hacia abajo en (a, b)
Punto de inflexión
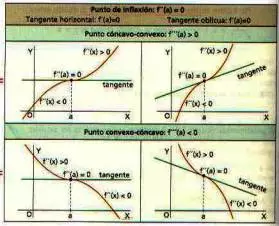
Gráfica con los casos de punto de inflexión de una función
Definición:
Un punto x0 se dice de inflexión de f si la función en ese punto cambia de concavidad, es decir, pasa de cóncava a convexa o de convexa a cóncava. Por tanto, en ese punto (x0, f(x0)) la tangente atraviesa la gráfica.
Condición necesaria: Si x0 es punto de inflexión entonces f"(x0) = 0
Condición suficiente: Sea x0/f"(x0) = 0, entonces si además f‴(x0) ≠ 0, x0 es punto de inflexión.
Regla de L'Hospital
Sean f, g:[a, b] ⟶ ℜ dos funciones verificando:
i. f, g son derivables en (a, b)
ii. g'(x) ≠ 0 para todo x ∈ (a, b)
iii. Existe
| lim x ⟶ a | f'(x) | = l ∈ ℜ (real o ± ∞) |
| g'(x) |
iv. Entonces existe
| lim x ⟶ a | f(x) | = | lim x ⟶ a | g(x) = 0 |
| lim x ⟶ a | f(x) | Su valor es l | ||
| g(x) | ||||
Con este resultado se resuelven todos los casos de indeterminación del calculo de limites: 0/0, ∞/∞, ∞ - ∞, 0 * ∞, 1∞, ∞° y 0°
Representación de funciones
Esquema a seguir en la representación de funciones
| Propiedades de funciones obtenidas directamente | Caracterización | ||
| 1- | Dominio (D) de la función Recorrido (R) de la función | x ∈ D ⇔ Existe y tal que y = f(x) y ∈ ℜ ⇔ Existe x tal que y = f(x) | |
| 2- | Simetrías: | ||
| Función par Función impar | f(-x) = f(x) Eje de simetría OY f(-x) = -f(x) Centro de simetría el origen | ||
| 3- | Periodicidad | f(x + T) = f(x) T período mínimo | |
| 4- | Puntos de corte con los ejes: | ||
| Corte con el eje OX Corte con el eje OY | f(x) = 0 Ninguno, uno o más puntos f(0) = y Ninguno o un punto | ||
| 5- | Regiones de existencia de la función: | ||
| Intervalos de positividad Intervalos de negatividad | f(x) > 0 Gráfica por encima del eje OX f(x) < 0 Gráfica por debajo del eje OX | ||
| 6- | Ramas infinitas. Puntos en el infinito: | ||
| Punto de partida de la gráfica Punto de llegada de la gráfica | (- ∞,?) Cuadrantes II o III (+ ∞,?) Cuadrantes I o IV | ||
| 7- | Asíntotas: | ||
| Asíntotas verticales: x = u | lim x ⟶ a | f(x) = ± ∞ (a = a, a+, a¯) | |
| Asíntotas horizontales: y = k | lim x ⟶ ±∞ | f(x) = k | |
| Asíntotas oblicuas: y = m·x + n, m y n ∈ ℜ m ∈ ℜ | lim x ⟶ ± ∞ | f(x)/x = m | |
| lim x ⟶ ± ∞ | [f(x) - m·x = b] | ||
| 8- | Puntos de discontinuidad | lim x ⟶ a | f(x) ≠ f(a) |
| Propiedades de f obtenidas por las derivadas sucesivas | |||
| 9- | Monotonía: | ||
| Intervalos de crecimiento Intervalos de decrecimiento | f' > 0 f' < 0 | ||
| Puntos críticos | f'(a) = 0 y f"(a) > 0 Mínimo f'(a) = 0 y f"(a) < 0 Máximo | ||
| 10- | Curvatura: | ||
| Intervalos de convexidad Intervalos de concavidad | f" > 0 f" < 0 | ||
| Puntos de inflexión | f"(a) = 0 y f"(a) > 0 Cóncavo - convexo f"(a) = 0 y f"(a) < 0 Convexo - cóncavo | ||
Autor: Sin datos
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
- ‹ Anterior
- |
- Siguiente ›
¿Qué son los valores máximos y mínimos de una función? ¿Qué es el incremento de la función?