Medición potenciométrica
El problema es determinar la fem de X.
V: fuente estable.
G: galvanómetro.
X: fuente desconocida.
P: fuente conocida.
1. Circuito cerrado
V = constante
I = constante
Se corre el cursor hasta que G = 0.
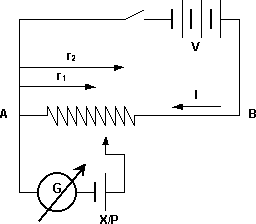
Circuito básico de medición potenciométrica
Entonces:
Ex = I·R1
Se cambia la fuente desconocida (X) por otra conocida (P).
| Ex | = | I·R1 | = | r1 |
| EP | I·R2 | r2 |
| Ex | = | r1 |
| EP | r2 |
Leyes de Kirchhoff
Si un circuito tiene un número de derivaciones interconectadas, es necesario aplicar otras dos leyes para obtener el flujo de corriente que recorre las distintas derivaciones.
1° ley de Kirchhoff:
La ley de los nudos o nodos, enuncia que en cualquier unión en un circuito a través del cual fluye una corriente constante, la suma de las intensidades que llegan a un nudo es igual a la suma de las intensidades que salen del mismo.
∑i = 0 (en un nodo)
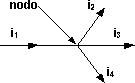
i1 = i2 + i3 + i4
2° ley de Kirchhoff:
La ley de las mallas afirma que, comenzando por cualquier punto de una red y siguiendo cualquier trayecto cerrado de vuelta al punto inicial, la suma neta de las fuerzas electromotrices halladas será igual a la suma neta de los productos de las resistencias halladas y de las intensidades que fluyen a través de ellas. Esta segunda ley es sencillamente una ampliación de la ley de Ohm.
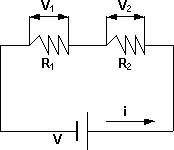
Circuito eléctrico con resistencias en serie
∑(V + fem) = 0 (en una malla)
V - V1 - V2 = 0
En un elemento activo el sentido de la corriente y de la tensión son iguales.
En un elemento pasivo el sentido de la tensión es inverso al de la corriente.
Vi = i1·R1 + i2·R2 + i3·R3 = Vf
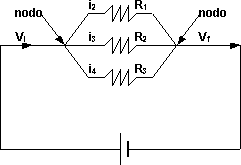
Circuito eléctrico con resistencias en paralelo
Trabajo eléctrico
L = q·V
| P = | L |
| t |
| P = | q·V |
| t |
P = i·V
Como:
V = i·R
P = i²·R
También:
| i = | V |
| R |
| P = | V² |
| R |
[P] = W
Otra unidad es el elctrón volt: es la energía adquirida por una partícula cuya carga es igual a la de un electrón, cuando esa partícula pasa por una diferencia de potencial de un volt en el vacío.
qe = 1,6·10-19 C
L = qe·V
L = 1,6·10-19 C·1 V
L = 1,6·10-19 J
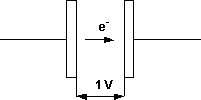
Representación de un capacitor
1 eV = 1,6·10-19 J
En serie:
P1 = i²·R1
P1 = (2 A)²·1 Ω
P1 = 4 A²·1 Ω
P1 = 4 W
P2 = i²·R2
P2 = (2 A)²·2 Ω
P2 = 4 A²·2 Ω
P2 = 8 W
En paralelo:
P1 = i1²·R1
P1 = (6 A)²·1 Ω
P1 = 36 A²·1 Ω
P1 = 36 W
P2 = i2²·R2
P2 = (3 A)²·2 Ω
P2 = 9 A²·2 Ω
P2 = 18 W
V = E + I·Ri
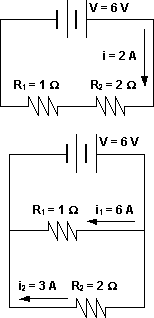
Circuito eléctrico con resistencias en serie y en paralelo
P = V·I
P = E·I + I·Ri·I
P = E·I + I²·Ri
En carga:
P = E·I + I²·Ri
E·I: rapidez de carga
I²·Ri: rapidez de pérdida
En consumo:
P = E·I + I²·Ri
E·I: rapidez de conversión de energía química en eléctrica.
I²·Ri: pérdida por calor
Autor: Ricardo Santiago Netto. Argentina
¿Qué dice la primera ley de Kirchhoff?