Refractómetro - Ensayo
1. Objetivos de la práctica:
a) Cálculo del ángulo refringente α, y del ángulo de mínima desviación δm
b) Obtener experimentalmente el índice de refracción de un prisma dado, para diferentes longitudes de onda de una lampara de sodio
c) Dibujar la curva de dispersión del vidrio (mediante la Ecuación de Cauchy)
2. Introducción:
Esta experiencia se apoya en el hecho de que el índice de refracción, de un material, es diferente para cada color de la luz que se propaga en dicho material. Este fenómeno se llama dispersión cromática.
Disponemos de un prisma dispersor, un goniómetro y una lampara de sodio a baja presión. El goniómetro es un instrumento que nos da la medida de ángulos por métodos óptico-geométricos. Antes de empezar las medidas deberemos calibrar dicho instrumento. Para ello enfocaremos el anteojo en el infinito y ajustaremos la abertura del colimador, para ver lo mejor posible las líneas espectrales.
El prisma que utilizaremos es capaz de separar un haz de luz policromática en sus frecuencias constituyentes, el índice de refracción dependerá de la frecuencia del haz incidente.
El desarrollo de esta práctica se basa en la ley de Snell de la reflexión y refracción y en la teoría de la dispersión cromática. Esta última nos índica que si consideramos la constante de amortiguamiento muy pequeña, podemos aproximar el índice de refracción de un DHI
nr(ω) = 1 + (Ne²/2·m·ε0)·[(ω0² - ω²)/((ω0² - ω²) + δ² ω²)]
a)
nr(ω) = 1 + (Ne²/2·m ε0)·(1/(ω0² - ω²))
Si además escribimos
ω = 2·π·c/1 ω0 = 2·π·c/λ0·P = Ne²·λ0²/2·m·ε0(2·π·c)²
Obtenemos la Ecuación de Sellmeier
nr(λ) = 1 + P·λ²/(λ² - λ0²)
Considerando ω << ω0 y desarrollando en serie de potencias, llegamos a la Ecuación de Cauchy:
nr(λ) = A + B/λ²
Esta ecuación nos dice que el índice de refracción, para estos medios, es diferente para las diferentes frecuencias de la luz policromática incidente.
Para la obtención de n(λ) veremos que, cuando incide el haz de luz en el prisma, el haz sufre una desviación con respecto a la dirección de incidencia (δ). Como vemos en el dibujo
δ = (Φi1 - Φt1) + (Φi2 - Φt2) y α = Φt1 + Φi2 por tanto δ = Φi1 + Φt2 + α
3. Determinación del ángulo refringente α.
Situaremos la arista refringente del prisma (la que une las dos caras transparentes del prisma) frente al colimador del goniómetro. Buscamos con el ocular la línea que procede de la reflexión en el prisma y, como vemos en el dibujo, calculamos α, que cumple la relación α = Φ/2.
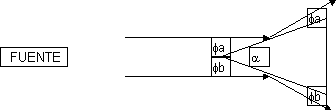
Nosotros medimos Φa y Φb en las dos escalas que tenemos y a partir de ellas obtenemos:
| Φa | Φb | α = Φ/2 | |
|---|---|---|---|
| Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 195° 40' ± 1' 15° 00' ± 1' 173° 16 ± 1" 353° 14' ± 1' 197° 04' ± 1' 17° 00' ± 1' 200° 05' ± 1' 20° 04' ± 1' 191° 11' ± 1' 11° 07' ± 1' | 75° 00' ± 1' 255° 00' ± 1' 53° 14' ± 1' 233° 16' ± 1' 77° 03' ± 1' 257° 04' ± 1' 80° 08' ± 1' 260° 05' ± 1' 71° 10' ± 1' 251° 11' ± 1' | 60° 20' ± 1' 60° 00' ± 1' 60° 45' ± 1' 59° 59' ± 1' 60° 01' ± 1' 59° 58' ± 1' 59° 59' ± 1' 60° 00 ± 1' 59° 56' ± 1' 60° 23' ± 1' |
αmedia = 60° 01' desviación stand σ(α) = 16,10'
Consideramos como error la desviación estadística σ (x).
4. Determinación del ángulo de mínima desviación:
Lo primero en este apartado será girar el prisma, hasta obtener las líneas procedentes de la refracción, que corresponderán a diferentes frecuencias. Tenemos los diferentes colores: Rojo, amarillo \ anaranjado, verde, verde débil, azul, azul débil, violeta.
El ángulo de mínima desviación se observa cuando, al girar el prisma, la línea se desplaza hasta un punto en el cual empieza a retroceder. En este punto tomamos la medida que corresponde al ángulo δm. Este procedimiento se repite para cada línea en cada escala (Dcha. e Izqda., cambiando la dirección del ángulo δm).
En las siguientes tablas vemos los valores medidos Φ1, Φ2 y δm:
| Φ1 | Φ2 | δm | |
|---|---|---|---|
| Escala 1 Escala 1 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 43,00 ±1' 42,87 ±1' 6,23 ±1' 186,32 ±1' 6,25 ±1' 186,28 ±1' 6,37 ±1' 186,30 ±1' | -53,03 ±1' -53,02 ±1' -89,77 ±1' 90,23 ±1' -89,73 ±1' 90,25 ±1' -89,67 ±1' 90,33 ±1' | 48,02 ±1' 47,95 ±1' 48,00 ±1' 48,04 ±1' 47,99 ±1' 48,02 ±1' 48,02 ±1' 47,98 ±1' |
δm media = 48,00 desviación standard σ(δm) = 0,03
| Φ1 | Φ2 | δm | |
|---|---|---|---|
| Escala 1 Escala 1 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 43,20 ±1' 43,17 ±1' 6,45 ±1' 186,50 ±1' 6,50 ±1' 186,50 ±1' 6,50 ±1' 186,48 ±1' | -53,22 ±1' -53,12 ±1' -89,95 ±1' 90,07 ±1' -89,93 ±1' 90,08 ±1' -89,90 ±1' 90,01 ±1' | 48,21 ±1' 48,15 ±1' 48,20 ±1' 48,22 ±1' 48,22 ±1' 48,21 ±1' 48,19 ±1' 48,19 ±1' |
δm media = 48,20 desviación standard σ(δm) = 0,03
| Φ1 | Φ2 | δm | |
|---|---|---|---|
| Escala 1 Escala 1 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 43,34 ±1 43,38 ±1 6,67 ±1 186,68 ±1 6,67 ±1 186,65 ±1 6,65 ±1 186,63 ±1 | -53,38 ± 1' -53,40 ± 1' -90,13 ± 1' 89,90 ± 1' -90,08 ± 1' 89,9 ± 1' -90,80 ± 1' 89,92 ± 1' | 48,36 ± 1' 48,39 ± 1' 48,40 ± 1' 48,39 ± 1' 48,38 ± 1' 48,38 ± 1' 48,37 ± 1' 48,36 ± 1' |
δm media = 48,38 desviación standard σ(δm) = 0,02
| Φ1 | Φ2 | δm | |
|---|---|---|---|
| Escala 1 Escala 1 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 43,97 ±1' 43,88 ±1' 7,35 ±1' 187,37 ±1' 7,25 ±1' 187,25 ±1' 7,25 ±1' 187,23 ±1' | -53,97 ± 1' -54 ± 1' -90,73 ± 1' 89,33 ± 1' -90,68 ± 1' 89,32 ± 1' -90,67 ± 1' 89,33 ± 1' | 48,97 ± 1' 48,94 ± 1' 49,04 ± 1' 49,02 ± 1' 48,97 ± 1' 48,97 ± 1' 48,96 ± 1' 48,95 ± 1' |
δm media = 48,98 desviación standard σ(δm) = 0,04
| Φ1 | Φ2 | δm | |
|---|---|---|---|
| Escala 1 Escala 1 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 44,17 ±1' 44,20 ±1' 7,52 ±1' 187,55 ±1' 7,50 ±1' 187,53 ±1' 7,52 ±1' 187,52 ±1' | -54,23 ±1' -54,23 ±1' -90,95 ±1' 89,03 ±1' -90,93 ±1' 89,05 ±1' -90,92 ±1' 89,08 ±1' | 49,20 ±1' 49,22 ±1' 49,24 ±1' 49,26 ±1' 49,22 ±1' 49,24 ±1' 49,22 ±1' 49,22 ±1' |
δm media = 49,23 desviación standard σ(δm) = 0,02
| Φ1 | Φ2 | δm | |
|---|---|---|---|
| Escala 1 Escala 1 Escala 1 Escala 2 Escala 1 Escala 2 Escala 1 Escala 2 | 44,68 ±1' 44,73 ±1' 8,03 ±1' 188,03 ±1' 8,67 ±1' 188,08 ±1' 8,02 ±1' 188,03 ±1' | -54,77 ±1' -54,77 ±1' -91,48 ±1' 88,51 ±1' -91,08 ±1' 88,55 ±1' -91,45 ±1' 88,55 ±1' | 49,73 ±1' 49,75 ±1' 49,76 ±1' 49,76 ±1' 49,87 ±1' 49,77 ±1' 49,74 ±1' 49,74 ±1' |
δm media = 49,77 desviación standard σ(δm) = 0,05
En la siguiente tabla vemos mejor el resultado de estas tablas:
| λ (Ångström) | δm | |
|---|---|---|
| Rojo Amarillo/Anaranjado Verde Verde débil Azul Violeta | 6.161 5.896 5.688 5.153 4.983 4.667 | 48,00 ± 0,03 48,20 ± 0,03 48,38 ± 0,02 48,98 ± 0,04 49,23 ± 0,02 49,77 ± 0,05 |
Los valores correspondientes al color azul débil fueron difíciles de observar y nos dieron resultados muy malos (probablemente nos confundimos al tomarlos), así que no los incluimos en la memoria. El error del ángulo de mínima desviación es la desviación estadística, mientras que el error de cada medida es de 1 minuto, 0,016 grados.
5. Determinación del índice de refracción n(α):
Cuando disponemos de α y δm podemos obtener el índice n(α) para cada longitud de onda mediante la expresión:
n(λ) = sen ((δm(λ) + α)/2)/sen (α/2)
El error de este índice lo calculamos mediante el estudio de la propagación de incertidumbre:
σ·n(λ) =
[(cos (δm + α)/2)/2·sen (α/2)]·σ·(δm) + [(cos (δm + α)/2)·sen (α/2)·sen (δm + α)/2)·cos (α/2))/sen ² (α/2)]δ(α)
Finalmente se presentan los resultados de los ángulos de mínima desviación y del índice de refracción para cada longitud de onda.
| λ (Ångström) | δm | n(λ) | |
|---|---|---|---|
| Rojo Amarillo/Anaranjado Verde Verde débil Azul Violeta | 6.161 5.896 5.688 5.153 4.983 4.667 | 48,00 ± 0,03 48,20 ± 0,03 48,38 ± 0,02 48,98 ± 0,04 49,23 ± 0,02 49,47 ± 0,05 | 1,6178 ± 0,0015 1,6198 ± 0,0019 1,6217 ± 0,0017 1,6278 ± 0,0020 1,6303 ± 0,0017 1,6412 ± 0,0018 |
Como vemos el ángulo de mínima desviación crece a medida que lo hace la frecuencia, o lo que es lo mismo, según va disminuyendo la longitud de onda. Por su parte el índice de refracción crece cuando lo hace δm, dicho índice sigue la ecuación de Cauchy. Según ésta ecuación n(λ) depende del inverso del cuadrado de la longitud de onda λ.
A continuación representaremos la curva de dispersión del vidrio, para ello recuperaremos la ecuación de Cauchy de la introducción.
nr(λ) = A + B/λ²
El resultado del ajuste por mínimos cuadrados de ésta ecuación es el siguiente:
A = 1,5881899
B = 1.088.606,1
r² = 0,971144603
En la gráfica adjunta se ve la curva de describe dicha ecuación con sus bandas de error, (error estadístico calculado por el TBLCURVE). Los datos se ajustan bastante bien a la curva aunque el coeficiente de correlación al cuadrado no es demasiado bueno.
Autor: Sin datos
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
Prácticas y ensayos de laboratorio.