Problema n° 4 de regresión lineal - TP05
Enunciado del ejercicio n° 4
En el siguiente cuadro se indican las cantidades de nitrógeno en el suelo después de su tratamiento con compost de residuos urbanos. Para cada uno de los niveles de tratamiento: 0, 4, 12 y 36 tn/ha de compost se realizaron 4 determinaciones. Los resultados fueron los siguientes:
| Dosis compost | Total nitrógeno (ppm) | |||
| 0 4 12 36 | 0,153 0,195 0,195 0,188 | 0,153 0,185 0,165 0,214 | 0,152 0,150 0,200 0,204 | 0,140 0,175 0,175 0,199 |
Estadísticas de la regresión
| Coeficiente de correlación múltiple Coeficiente de determinación R² R² ajustado Error típico Observaciones | 0,73446676 0,53944142 0,50654438 0,0161856 16 |
| Grados de libertad | Suma de cuadrados | Promedio de los cuadrados | F | Valor crítico de F | |
| Regresión | 1 | 0,00429581 | 0,00429581 | 16.3978702 | 0,00119459 |
| Residuos | 14 | 0,00366763 | 0,00026197 | ||
| Total | 15 | 0,00796344 |
| Coeficientes | Error típico | Estadístico t | Probabilidad | Inferior 95 % | Superior 95 % | |
| Intercepción | 0,16243333 | 0,00552843 | 29,3814383 | 5,5609·10-14 | 0,15057601 | 0,17429065 |
| Compost | 0,0011734 | 0,00028977 | 4,04942838 | 0,00119459 | 0,0005519 | 0,00179489 |
| Observación | Pronóstico Total Nitrógeno | Residuos |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | 0,16243333 0,16243333 0,16243333 0,16243333 0,16712692 0,16712692 0,16712692 0,16712692 0,1765141 0,1765141 0,1765141 0,1765141 0,20467564 0,20467564 0,20467564 0,20467564 | -0,00943333 -0,00943333 -0,01043333 -0,02243333 0,02787308 0,01787308 -0,01712692 0,00787308 0,0184859 -0,0115141 0,0234859 -0,0015141 -0,01667564 0,00932436 -0,00067564 -0,00567564 |
| Comp. X | Total Nitrógeno Y | Xi - X | Yi - Y | (Xi - X)·(Yi- Y) | (Xi - X)² | Pronóstico (Y sombrero) | x·y | x² | e = y - ŷ | (y - ŷ)² |
| 0 0 0 0 4 4 4 4 12 12 12 12 36 36 36 36 | 0,153 0,153 0,152 0,140 0,195 0,185 0,150 0,175 0,195 0,165 0,200 0,175 0,188 0,214 0,204 0,199 | -13 -13 -13 -13 -9 -9 -9 -9 -1 -1 -1 -1 23 23 23 23 | -0,025 -0,025 -0,026 -0,038 0,017 0,007 -0,028 -0,003 0,017 -0,013 0,022 -0,003 0,010 0,036 0,026 0,021 | 0,321 0,321 0,334 0,490 -0,156 -0,066 0,249 0,024 -0,017 0,013 -0,022 0,003 0,237 0,835 0,605 0,490 | 169 169 169 169 81 81 81 81 1 1 1 1 529 529 529 529 | 0,1628 0,1628 0,1628 0,1628 0,1674 0,1674 0,1674 0,1674 0,1768 0,1768 0,1768 0,1768 0,2050 0,2050 0,2050 0,2050 | 0 0 0 0 0,78 0,74 0,6 0,7 2,34 1,98 2,4 2,1 6,768 7,704 7,344 7,164 | 0 0 0 0 16 16 16 16 144 144 144 144 1.296 1.296 1.296 1.296 | -0,0098 -0,0098 -0,0108 -0,0228 0,0276 0,0176 -0,0174 0,0076 0,0182 -0,0118 0,0232 -0,0018 -0,0170 0,0090 -0,0010 -0,0060 | 0,000095 0,000095 0,000116 0,000518 0,000759 0,000308 0,000304 0,000057 0,000330 0,000140 0,000537 0,000003 0,000289 0,000081 0,000001 0,000036 |
| 208 | 2,843 | Sumas | 3,661 | 3.120 | 40,62 | 5.824 | SCE = | 0,003669 | ||
| CME = SCE/GLE = SCE/(n-2) | ||||||||||
| CME = | 0,000262 | |||||||||
| x | Y | b1 = 3,661/3.120 = | 0,001173 | b1 = (40,62-(208·2,843/16))/(5.824 - (208·208/16)) | ||||||
| 13 | 0,178 | b0 = 0,178 - 0,001173·13 = | 0,162751 | b1 = | 0,00117 | |||||
| b0 = (1/16)·(2,843 - 0,001173·208) | ||||||||||
| b0 = | 0,16244 | |||||||||
a)
Identifique las variables.
Y = nitrógeno en el suelo (variable independiente)
X = dosis de compost de residuos urbanos (variable dependiente o respuesta)
b)
Realice el gráfico de dispersión y comente.
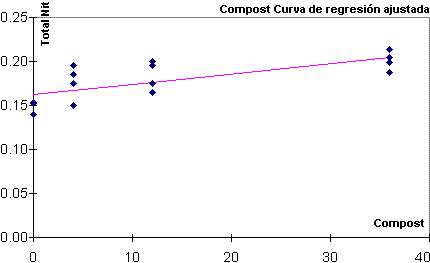
c)
Escriba el modelo lineal correspondiente y describa cada parámetro en términos del problema.
Yi = β0 + β1·Xi + εi
b0 = estimador de ordenada al origen = 0,16243333
b1 = estimador de pendiente = 0,0011734
Calcule y grafique la recta de regresión
Ŷ = 0,16243333 + 0,0011734·x
Gráfico en b)
d)
Compruebe la significación de los parámetros planteando las hipótesis asociadas.
| Valor p | |
| Intercepción | 5,5609·10-14 |
| Compost | 0,00119459 |
Los dos valores p son menores que 0,05 entonces ambos parámetros son significativos.
e)
Estime los parámetros por medio de intervalos de confianza.
Para β0
| 0,15057601 | 0,17429065 |
Para β1
| 0,0005519 | 0,00179489 |
f)
Estime la varianza poblacional.
Estimador de la varianza poblacional = CME = 0,00026197
Para una dosis de 3 Tn/Ha de compost, ¿cuál sería el total de nitrógeno en el suelo? ¿Y para una dosis de 50 Tn/Ha?
y(3) = 0,16243333 + 0,0011734·3 = 0,16595353
Si X = 50 entonces fuera de rango
g)
Calcule el error para la 5ta observación.
Y(5) esperado = 0,16243333 + 0,0011734·4 = 0,16712693
Y(5) observado = 0,195
e(5) = 0,195 - 0,16712693 = 0,02787307
h)
Calcule e interprete el coeficiente de determinación
El 53,94 % de las variaciones de nitrógeno en el suelo están explicados por las variaciones en las dosis de compost.
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
Ejemplo, cómo analizar la regresión lineal y cómo calcular la varianza poblacional y el intervalo de confianza