Modelos de examen parcial de Análisis Matemático II.
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Dada f:D ⊂ ℜn ⟶ ℜ(n > 1), A punto interior a D y r ⊂ ℜn, se debe realizar la derivada direccional f'(A, r)
a) Cuando es posible calcularla usando el ∇f? Justifique respuesta
b) Siendo:
| f(x, y) = | √xy | Si | x·y ≥ 0 |
| x + y | Si | x·y < 0 |
Halle los seis versores para los cuales la derivada direccional es nula en (0, 0).
Problema n° 2
Sean f:ℜ ⟶ ℜ y g:ℜ² ⟶ ℜ ambas C²; si se construye h = f o g, analizando únicamente mediante el Hessiano. En que casos los puntos para los que g produce máximos (mínimos) la función h produce máximos?
Problema n° 3
Calcule el flujo de f(x, y, z) = (y, x² - y, x·y) a través del trozo de superficie cilíndrica de ecuación y = x² en el primer octante, con x + y + z ≤ 2. Indique claramente en un gráfico la orientación que usted ha elegido para n.
Problema n° 4
Sea f un campo de gradientes con matriz jacobiana:
| Df(x, y) = | -6·x | 1 | ||
| 1 | 0 |
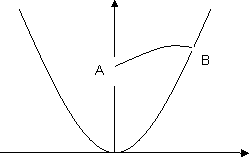
Sabiendo que la gráfica de su función potencial pasa por (1,2,1) con plano tangente x - y + z = 0, demuestre que la circulación de f a lo largo de cualquier curva que une un punto A del eje y con otro punto B de la parábola y = x² resulta nula.
Problema n° 5
Calcule la masa del cuerpo limitado por x² + z = 2, z = x² + 2·y², en el primer octante, si su densidad en cada punto es proporcional a la distancia desde el punto al eje.
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Dada g:D ⊂ ℜ² ⟶ ℜ/g(x, y) = √f(x, y), siendo f:ℜ² ⟶ ℜ/f(x, y) = x²·y² - x³·y.
a) Grafique D y demuestre que g(0, 0) es un mínimo absoluto de g(x, y) en D
b) Demuestre que f(0, 0) no es extremo relativo ni absoluto de f(x, y) en ℜ²
Problema n° 2
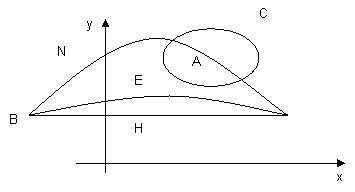
Sea f: ℜ² - {A} ⟶ ℜ², f tiene derivadas continuas y cumple la condición de simetría en su dominio.
Se sabe además que las integrales de línea ∫C+ f = 4 y ∫DHB f = 6.
Calcule justificando su procedimiento: ∫DHB f y ∫DEB f
Problema n° 3
Calcule el flujo de f(x, y, z) = ((x²·y,81 - x)·ex·z - 1,(1 - x)·ez - y) a través de la superficie frontera del cuerpo limitado por
z ≥ x², x + z ≤ 2, y ≤ 4, en el primer octante.
Problema n° 4
Sea C la curva definida como intersección de las superficies ex·z - 1 - x·y + ln (y·z) = 0 con y = x², si r0 es la recta tangente a C en A = (1, 1, 1). Calcule la distancia desde A hasta el punto en que r0 corta al plano de ecuación x + y = 8.
Problema n° 5
Calcule la circulación del campo f cuyo rot(f) = (x - y, y - x, -2·z) a lo largo de la curva de ecuación X = g(t) con t ⊂ [0,2·π], cuando g(t) = (3·cos t, 3·sen t, 6 - 3·cos t - 3·sen t).
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Dada u(x, y) = y. f(x/y) con f ⊂ C², demuestre que X = (x, y) es tangente a la línea de nivel de u'x que pasa por X.
Problema n° 2
Sea f:ℜ² ⟶ ℜ con matriz jacobiana contínua y simétrica en ℜ², demuestre que la circulación de f no depende del camino.
Problema n° 3
Determine los valores de a y b que minimizan el flujo de f(x, y, z) = (a²·x + b·y, b²·y + a·x, a·x·y - 4·(b - a)·z)
a través de la superficie frontera del cuerpo definido por 2·x² + 2·y² ≤ z ≤ 8, y calcule el valor de dicho flujo mínimo.
Problema n° 4
Si (div f)(x, y, z) = 2·y calcule el flujo de f a través del casquete de esfera de ecuación x = (4 - y² - z²)½ sabiendo que f(0, y, z) = (ey² + z², z, y²). Indique claramente en un esquema la orientación del versor normal elegido.
Problema n° 5
Dada la superficie S de ecuación X = (u·(v + 8/9)3/2, u - v, u·v) con (u, v) ⊂ ℜx[-8/9, ∞], calcule la longitud del trozo de línea coordenada de u = 1 cuyos puntos están en el primer octante.
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Sea φ ⊂ C²(ℜ³), demuestre que F = φ∇φ es un campo de gradientes, y calcule ∫ λAB F·ds sabiendo que φ (B) = 7 y que ∫ λAB ∇φ·ds = 4 (Ā y B son los puntos inicial y final del arco de una curva suave λAB)
Problema n° 2
Considera los campos escalares f y g definidos en D ⊂ ℜn,Ā interior a D, g(Ā) = 0, f contínua en Ā.
Demuestre que si g es derivable respecto de ř en Ā, también lo es h = f·g, resultando h'(Ā, ř) = f(Ā)·g'(Ā,ř).
Problema n° 3
Calcule el flujo de f(x, y, z) = (z³, y·x², x·z²) a través del trozo de cilindro de ecuación x² + z² = 4 cuyos puntos cumplen con z ≥ (x² + 2·y)½. Indique en un esquema la orientación del n que ha elegido.
Problema n° 4
La ecuación 1 + x² - 2·x·z + y²·ez - 1 - ln z = 0 define implícitamente a z = f(x, y), analice la existencia de extremos relativos de los valores de f.
Problema n° 5
Calcule el momento estático del cuerpo H respecto del plano x, z si la densidad en cada punto es proporcional a la distancia desde el punto al plano x, z. H está en el primer octante definido por x + y + z ≤ 2, z ≥ x + y, y ≤ x.
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Sean Ā y B dos puntos de la superficie de nivel k del campo escalar f ⊂ C¹(ℜ³), demuestre que ∫C (∂f/∂T)·dS = 0 a lo largo de cualquier curva C suave con una Ā con B. (T es el versor tangente a C)
Problema n° 2
Calcule el flujo de f(x, y, z) = (P(y, z), y + z²,2·z - x) a través de la superficie frontera del cuerpo definido por
y ≥ 2·x², y ≤ 2, x + z ≤ 1, x ≥ 0, z ≥ 0; sabiendo que f ⊂ C¹(ℜ³).
Problema n° 3
Sea S la superficie de ecuación z = φ (x, y) definida implícitamente por y·z - x + ln z = 0, y π0 el plano tangente a S en su punto común con el eje Z. Determine los valores de a, b, c, d para que el plano de ecuación a·x + b·y + c·z = d que pasa por (1, 3, 0) sea paralelo al π0
Problema n° 4
Sea f ⊂ C¹(ℜ³) tal que f(x, 0, 0) = (x², 0, x) y rot f(x, y, z) = (2·y + 1, y - 1, -z). Calcule ∫C f·dS desde (2, 0, 0) hasta (-2, 0, 0) a lo largo de C intersección de
z = (4 - x²)½, con y = 0
Problema n° 5
Calcule el área del trozo de esfera de ecuación x² + y² + z² = 20 con z ≥ 2·(x² + y²)½
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Si f = rot(Ā), Demuestre que todo campo C¹(ℜ³), tiene flujo nulo a través de cualquier superficie S cerrada suave a trozos.
Problema n° 2
Dada 2·x·y + z + e² - 1 = 0 que define implícitamente a f(x, y), demuestre que f(x, y) ≈ - x·y en un E(0, 0).
Problema n° 3
Sea.
| f(x, y) = | y² - x² | Si | x ≥ 0 |
| (x + 1)² + y² | Si | x < 0 |
Grafique el conjunto de nivel 0, y analice si f(0, 0) es extremo relativo.
Problema n° 4
Calcule es área de la superficie frontera del cuerpo definido por: y ≤ x, x + y + z ≤ 2, primer octante.
Problema n° 5
Calcule el flujo de f a través del trozo de paraboloide de ecuación z = 4 - x² - y² con z ≥ 0, sabiendo que f(x, y, 0)·ǩ = 3·y que div(f(x, y, z)) = 3·x². Indique claramente en un esquema la orientación que ha elegido para el n al paraboloide.
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Sea f: ℜ² - {Ā} ⟶ ℜ² con matriz Jacobiana contínua y simétrica en su dominio. Considere curvas del tipo simple cerrada y suave a trozos, orientadas en sentido positivo y que no pasen por Ā.
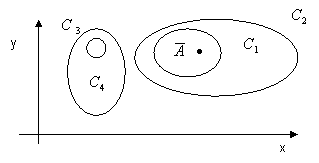
Demuestre que la circulación de f a lo largo de cualquier curva que rodea al punto Ā tiene el mismo valor; ídem para las que no lo rodean.
Es decir:
∮C1+ f·dS = ∮C2+ f·dS
y
∮C3+ f·dS = ∮C4+ f·dS
Problema n° 2
Calcule el área de la región D del plano x·y cuya frontera es la curva de ecuación X = g(t) con t ⊂ [-1, 3], siendo:
| g(t) = | (t, 0) (t, t²) (2 - t, (3 - t)/2) | Si si si | -1 ≤ t ≤ 0 0 ≤ t ≤ 1 1 ≤ t ≤ 3 |
Problema n° 3
Calcule el flujo de f(x, y, z) = (z³, y·z, x·z²) a través del trozo S de cilindro de ecuación z = (32 - x²)½ con y ≥ √3·x, z ≥ (x² + 2·y²)½, en el primer octante. Indique claramente en un esquema la orientación que ha elegido para el versor normal a S.
Problema n° 4
Calcule el volumen en el primer octante limitado por x² + y² = 4, z = x, y = x, y = 0.
Problema n° 5
Dada.
| f(x, y) = | x·y²/(x² - y²) | Si | |x| ≠ |y| |
| 0 | Si | |x| = |y| |
Demuestre que f es derivable en toda dirección en el origen, pero no es diferenciable en dicho punto.
Modelo de 2° Parcial para Análisis Matemático II
Problema n° 1
Sea f:D ⊂ ℜ² ⟶ ℜ/|f(x, y)| ≤ |x, y| ∀ (x, y) E(0). Demuestre que fes contínua y derivable en toda dirección en (0, 0).
Problema n° 2
Siendo w = x·y - x² con y = f(x) definida implícitamente por x + 2·y + ex·y - 4 = 0, resulta w = h(x). Calcule h(0,02) en forma aproximada usando diferencia total.
Problema n° 3
Calcule el área del trozo de esfera de ecuación x² + y² + z² = 2 con z ≥ x² + y², y ≥ x, x ≥ 0.
Problema n° 4
Halle el punto común a la recta r y el plano de ecuación z = x + 3·y, si r es la recta tangente a la curva definida por la intersección de las superficies de ecuación x² - y² + z = 0 y z = x - 5 en (2, 1, -3).
Problema n° 5
Calcule el momento estático respecto del plano x·y del cuerpo definido por x² + y² + z² ≤ 2 con y ≥ x² si la densidad en cada punto es proporcional a la distancia desde el punto al plano x, z
Autor: Sin datos
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)