Holografía: Introducción al holograma (4° parte)
Funciones matemáticas del holograma
Transformaciones de Fourier
En el siglo XIX, los matemáticos perfeccionaron una teoría conocida como el análisis de Fourier. Joseph Fourier, un matemático francés, afirmó en 1.807 que cualquier forma de onda repetitiva (o función periódica), se puede expresar como una suma infinita de ondas sinusoidales y cosinusoidales de diversas frecuencias. En óptica el análisis de Fourier (un sistema matemático de análisis de matrices y de sumas infinitas de expresiones trigonometricas) permite representar un objeto como una suma de componentes. A veces se analizan los sistemas ópticos escogiendo un objeto cuyas componentes de Fourier se conocen y analizando las componentes de Fourier de la imagen.
Posteriormente, los matemáticos ampliaron la idea de Fourier a funciones no periódicas (u ondas) que cambian en el tiempo, en lugar de repetirse en la misma forma para siempre. La mayoría de las ondas del mundo real son de este tipo. En las imágenes también es importante la distinción entre patrones repetitivos y no repetitivos. Un patrón repetitivo se puede ver como una textura o fondo, mientras que un patrón no repetitivo es percibido por el ojo como un objeto. Para representar patrones repetitivos (fondo) de una imagen se pueden utilizar ondas periódicas o repetitivas formadas por una serie de armónicos. Las características no repetitivas se pueden resolver en un espectro de frecuencias mucho más complejo, denominado "transformación de Fourier", de la misma forma que la luz se puede descomponer en un espectro de colores.
La transformación de Fourier representa la estructura de una onda periódica de forma mucho más reveladora y concentrada que lo haría el gráfico tradicional de una onda. Por ejemplo, una vibración de un motor aparecería como un pico de frecuencia inusual en la transformación de Fourier.
Gráfico de una onda
Gráfico de la vibración de un motor según la transformación de Fourier
En óptica las medidas de intensidad son las únicas experimentalmente realizables. La recuperación de la fase a partir de estas medidas es un problema importante en la ciencia moderna y en la computación óptica en particular. Las nuevas alternativas a la interferometría basadas en propagación de ondas en ciertos sistemas particulares aumentan las posibilidades de la medida de la fase. La distribución de Wigner (WD, que permite la representación de señales en el espacio tiempo (posición)-frecuencia.) es una herramienta importante, utilizada para análisis y caracterización de las señales (campos de ondas) en óptica, astronomía, mecánica cuántica, telecomunicaciones, tratamiento de imágenes, etc.
De forma generalizada, el campo óptico está caracterizando no por su WD, que es una función de 4 variables, si no por sus momentos. Es posible calcular el número mínimo de proyecciones de WD para estimar todos sus momentos globales hasta orden infinito. En general, la determinación óptica de WD o sus momentos globales y locales a partir de medidas de intensidad abre nuevas perspectivas para el procesado óptico de la información.
El filtrado óptico en los dominios fraccionarios, diferentes del dominio de Fourier, puede aplicarse al reconocimiento de imágenes espacio-variantes. Los resultados de nuestro estudio demuestran que, en la mayoría de los casos, la fase de la transformada de Fourier fraccionaria contiene más información de la imagen que su amplitud.
- La transformación de Fourier unidimensional
Si f(x) es una función contínua de variable real x, la transformada de Fourier de f(x) se define por la ecuación:
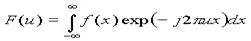
Dado F(u), f(x) puede calcularse utilizando la transformada inversa de Fourier:
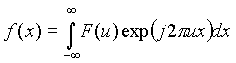
Estas dos ecuaciones, denominadas par de transformaciones de Fourier, existen si f(x) es contínua e integrable y F(u) es integrable. La transformada de Fourier de una función real, habitualmente es una función compleja:
F(u) = R(u) + j·I(u)
F(u) = |F(u)|·ej·I(u)
|F(u)| = [R²(u) + I²(u)]½
Φ(u) = tg⁻¹ [I(u)/R(u)]
A la función |F(u)| se la denomina módulo y (u) es la fase. A la variable (u) a veces se la denomina variable de frecuencia.
El holograma
Definición:
El holograma fue inventado por el físico e ingeniero húngaro Dennis Gabor quien fue galardonado con el premio Nóbel en 1.971 por su gran descubrimiento y aporte a la ciencia.
Su invento consta en un método de obtener imágenes fotográficas tridimensionales. Las imágenes se crean sin lente, por lo que también se denomina fotografía sin lente. Las grabaciones reciben el nombre de hologramas (en griego, holos, 'todo'; gram, 'mensaje').

Dennis Gabor
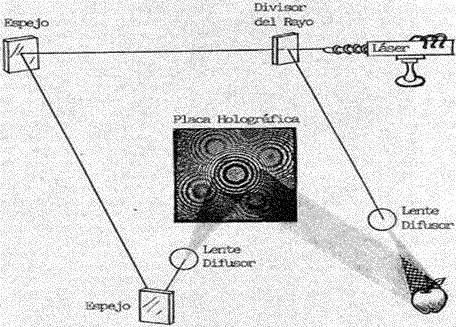
Es un registro fotográfico de la interferencia entre un haz de referencia y el diagrama de difracción del objeto. Para generar un holograma, la luz procedente de un único láser se divide en dos haces. El haz de referencia ilumina la placa fotográfica -por ejemplo, a través de una lente y un espejo- y el segundo haz ilumina el objeto. El haz de referencia y la luz reflejada por el objeto forman un diagrama de difracción sobre la placa holográfica.
Si una vez revelado el holograma se ilumina con luz coherente, no necesariamente de la misma longitud de onda que la empleada para crearlo, la imagen del objeto fotografiado aparece inmediatamente en el espacio, dando la ilusión del objeto restituido en sus tres dimensiones y permitiendo al espectador, según se vaya desplazando, ver, por ejemplo, los dos perfiles y la cara del modelo. Es posible producir hologramas de un objeto teórico mediante ordenadores o computadoras, y después pueden reconstruirse las imágenes de esos objetos.
Un holograma se diferencia básicamente de una fotografía normal en que no sólo registra la distribución de intensidades de la luz reflejada, sino también la de fases. Es decir, la película es capaz de distinguir entre las ondas que inciden en la superficie fotosensible hallándose en su amplitud máxima, de aquellas que lo hacen con amplitud mínima. Esta capacidad para diferenciar ondas con fases distintas se logra interfiriendo un haz de referencia con las ondas reflejadas.

Representación de un holograma
Podemos decir que la holografía es una técnica de formación de imágenes tridimensionales a partir de un soporte plano, que pueden ser vistas sin necesidad de ningún accesorio para el observador, y donde este puede moverse alrededor del soporte viendo al objeto, sin discontinuidades, dentro de un ángulo por donde se le ofrecen todas las perspectivas.
La holografía fue oficialmente descripta en 1.947 por Dennis Gabor, quien siguiendo una idea anterior llegó a la solución de un problema interesante: se trataba de que, iluminando una rendija con luz de un color único (luz verde de una lámpara de mercurio) se obtiene una figura de franjas que permite conocer la forma y dimensiones de la rendija. Teniendo la información, ¿qué sería necesario para ver la rendija? Ese proceso de decodificación de la información fotografiada lo resolvió Gabor pues planteó el mismo problema intentando mejorar la óptica de los microscópios electrónicos. Faltaba algo para registrar la inclinación de los rayos que llegan a la película fotográfica.
Normalmente, se registra la intensidad pero no se sabe en que dirección la luz llegó. Adicionando junto con la luz del objeto un haz de la misma luz sobre la película, que llamó de "haz de referencia", creó la técnica holográfica. En ese caso la cantidad de franjas se incrementa mucho más a medida que el ángulo de incidencia aumenta, y el registro, al ser iluminado por un haz semejante al de referencia, desvía la luz de manera exactamente igual a la que lo hace el objeto. Se complementan así con perfección dos fenómenos físicos: La interferencia y la difracción. Pero la holografía solamente fue reconocida como gran invención en 1.962 cuando, al disponerse de luz láser, se pudieron hacer imágenes grandes, nítidas, y con gran campo para la visión, mostrando diferentes puntos de vista. Gabor, ingeniero eléctrico, recibió el premio Nóbel de Física en 1.971.
Vale la pena comentar otros descubrimientos relacionados: En 1.891, Gabriel Jonas Lippmann en Francia presentó un proceso que lo llevó al premio Nóbel de 1.908, la "Fotografía Lippmann", que permitía que una placa fotográfica registrase los colores de una foto. La placa era del tipo usado en esa época para fotografía (no existía la fotografía en colores) y, casualmente, de altísima resolución, vários miles de líneas por milímetro, 40 veces mayor de lo que realmente una cámara fotográfica puede ofrecer. Al agregar la posibilidad de que la luz se reflejase inmediatamente después de atravesar la placa, Lippmann creaba figuras de interferencia donde la longitud de onda de la luz quedaba registrada, y se auto reproducía al iluminarla después con luz blanca. Si bien por motivos prácticos esta técnica no tuvo aplicación generalizada, su excelente carácter teórico, y otras experiencias donde Lippmann intentó obtener nuevas técnicas de imágenes tridimensionales superiores a la estereoscopía, ciertamente contribuyeron al desarrollo de la holografía.
En 1.958 el físico ruso Yuri Nikolaevich Denisyuk, leyendo un libro de ciencia ficción donde se narraba que restos de civilizaciones venidas de otros planetas incluían retratos perfectamente tridimensionales, intentó crear una técnica así, basado en la técnica de Lippmann y desconociendo la de Gabor. Consistía en agregar un haz de referencia, pero por detrás de la placa. Que solamente fue reconocida en 1.962, cuando la holografía fue noticia, y entonces la técnica de Denisyuk quedó como la primera que podía permitir la visualización de imágenes holográficas con luz blanca. El desafío actual de la holografía consiste poder registrar holográficamente con luz blanca, siendo que ya se ha conseguido proyectar sobre una pantalla con luz blanca.
Método holográfico
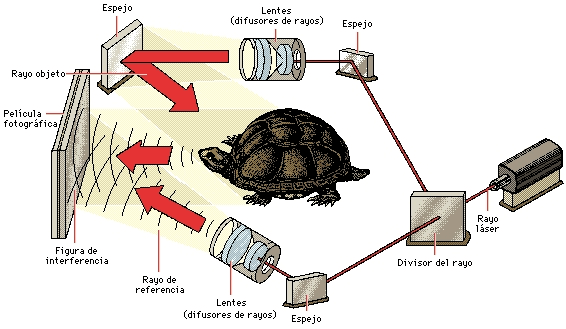
Uno de los métodos de obtención de hologramas, es iluminar el objeto mediante un haz de luz coherente (un haz en el que todas las ondas se desplazan en fase entre sí y que se genera con un láser). En esencia, la forma del objeto determina el aspecto de los frentes de onda, es decir, la fase con la que la luz reflejada incide en cada uno de los puntos de la placa holográfica.
Parte de este mismo haz láser se refleja simultáneamente en un espejo o prisma y se dirige hacia la placa fotográfica; este haz se denomina haz de referencia. Los frentes de onda de este último, al no reflejarse en el objeto, permanecen paralelos respecto del plano y producen un patrón de interferencia con los frentes de onda de la luz reflejada por el objeto. Si éste es un punto, por ejemplo, los frentes de onda del haz reflejado serán esféricos; el patrón de interferencia producido en la película estará entonces formado por círculos concéntricos, reduciéndose el espacio entre los círculos a medida que aumenta el radio.
El patrón de interferencia producido por un objeto más complicado también será mucho más complejo, por lo que el holograma resultante sólo descubrirá un complicado patrón de estructuras oscuras y claras que no tiene relación con el objeto original.

Método de obtención de hologramas mediante un haz de luz coherente
Sin embargo, si se contempla el holograma bajo luz coherente (iluminando la placa holográfica grabada con luz láser), se hará visible el objeto grabado; y si se contempla el holograma desde diferentes ángulos, el objeto también se ve desde distintos ángulos. El efecto tridimensional se consigue porque el holograma reconstruye en el espacio los frentes de onda que originalmente fueron creados por el objeto. Este mecanismo se puede entender a la vista del ejemplo del holograma de un punto.
La luz coherente que incide en los círculos concéntricos del holograma sufre una difracción sobre una rejilla de difracción. El ángulo del haz aumenta con la distancia respecto del centro de los anillos concéntricos, reconstruyendo así los frentes esféricos de onda, y el espectador percibe el punto en la misma ubicación relativa en la que se hallaba el punto real al construir el holograma.
Los frentes de onda de los objetos más complejos se reconstruyen de la misma forma. La distribución de intensidades de la luz reflejada se registra en el grado de oscurecimiento de los patrones de interferencias de la película.
Si el objeto ha sufrido alguna deformación entre ambas grabaciones, aparecerán diferencias de fase en determinadas zonas de las dos imágenes, creando un patrón de interferencias que mostrará claramente dicha deformación.
La placa en la que se graba el holograma recoge un patrón de interferencias, formadas por el entrechocar de ondas luminosas; en este caso, si se observara directamente una placa holográfica lo que se vería sería sólo eso: un patrón difuso, un caos luminoso sin ningún sentido ni forma. La astucia de los inventores de la fotografía holográfica, Leith y Upatnicks, fue emplear un rayo de luz coherente para que surja, de entre esa confusión luminosa, la imagen nítida y tridimensional del objeto que se fotografió.
La codificación y decodificación de frecuencias es precisamente la especialidad del holograma. Este emplea para el descifrado de las percepciones el lenguaje matemático conocido como "transformaciones de Fourier" utilizado en la elaboración de hologramas laserianos.
Esquema del holograma de transmisión
Se pueden realizar dos tipos de hologramas: hologramas de reflexión y hologramas de transmisión, que se diferencian según como la imagen registrada en el holograma se reconstruya, si por reflexión o por transmisión del haz de lectura sobre el holograma. El tipo de holograma requerido se obtiene cambiando la disposición experimental durante el registro holográfico.
Esquema del holograma de reflexión
En los hologramas de reflexión el haz objeto y el de referencia inciden sobre caras distintas de la placa holográfica, mientras que en los hologramas de transmisión ambos haces inciden sobre la misma cara (la cara de la emulsión).
Entonces con el holograma se obtiene una fotografía tridimensional, o más bien, como se dice hoy en día, un sistema óptico -sin lentes- de almacenamiento y recuperación de la información. Su peculiaridad reside en que toda la imagen se encuentra en cualquier parte del soporte fotosensible -el análogo de la película fotográfica de las fotos clásicas bidimensionales- de forma que si se parte una imagen por la mitad, en cada una de las dos mitades aparecerá la imagen original entera.
Esquema del holograma de reflexión
Cálculo de los frentes de onda
Amplitud resultante Cuando se ilumina la superficie con un haz y se observa desde un plano V, se tiene una amplitud:
∑u₂(P) = u₀ = A ∈ C (P, ε) = (eⁱ˙ᵏᵢ⁻ᵏₛ)·(P·A + d)
La amplitud resultante es:
∑ A ∈ C (P, ε) = (eⁱ˙ᵏᵢ·⁻ᵏₛ)·P·A+(eⁱ˙ᵏᵢ·⁻ᵏₛ)·(P·A + d))
La intensidad resultante es:
∑u·u' = u₀² = A ∈ C(P, ε) = (2 + 2·cos k·C·d) + …
Franjas Cuando se observa desde un punto de vista V, las franjas aparecen espaciadas de modo que si: N = 1/λ = C·d
Enfoque de las franjas Los puntos en los que: cos k·C·d = (2·n + 1)·π
Se observarán franjas oscuras si cos k·C·d se mantiene más o menos constante en todo el área de resolución, es decir, si N = kC·d verifica que:
∂N/∂x₂ = Δx₂, = ∂N/∂x₃ = Δx₃
Son pequeñas, lo que no se cumplirá, en general, para cualquier V, por lo que las franjas sólo se observarán en determinadas posiciones.
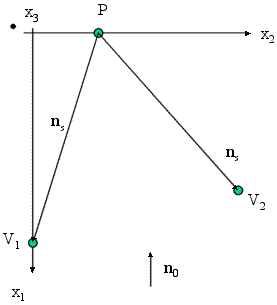
Cálculo de los frentes de ondas
Cálculo de los coeficientes
C = [X₁² + (X₂ - x₂)² + x₃²]½ X₁·e₁ + (X₂ - x₂)·e₂ - x₃·e₃ + e₁
R = [X₁² + (X₂ - x₂)² + x₃²]½ = ∂1/R/∂x₂ = X₂ - x₂/R³ = ∂1/R/∂x₃ = x₃/R³
Oscilaciones
Sea una oscilación de pulsación ω y amplitud a₀, que determina una amplitud de interferencia en la superficie de grabación: u = uᵣ·exp iφᵣ + u₀·exp(i·φ₀ + 2·i·ka₀·sen ω·t)
y una intensidad: I = uᵣ·u'ᵣ + u₀·u'₀ + 2·u₀·uᵣ·cos (φ₀-φᵣ + 2·ka₀·sen ω·t)
Cuyo promedio temporal es: < I > = uᵣ·u'ᵣ + u₀·u'₀ + 2·u₀·uᵣ·cos (φ₀ - φᵣ)·J₀(2·ka₀)
Con lo que la imagen virtual reconstruida: u'rec = 2·k·u₀ uᵣ²·J₀·(2·ka₀)
Aparece modulada por la función J₀·(2·ka₀), lo que proporciona franjas oscuras para los ceros de J₀·(2·ka₀).
Laboratorio de holografía (práctica)
Técnicas de laboratorio, equipo y características holográficas
Holografía con lásers de diodo
Las mejoras en los lásers de diodo, con potencias superiores en el espectro visible, pueden hacer que los lásers de He-Ne se vuelvan obsoletos. En estos momentos, la coherencia de estos lásers es algo limitada, pero, sin embargo, permiten realizar algunos hologramas impresionantes. Las aplicaciones de la formación y no formación de imágenes (es decir, mostrar la longitud de coherencia y la eficiencia de difracción) son dos posibles proyectos.
Sensibilidad de la luz ambiente
Las placas holográficas son relativamente poco sensibles a la luz. Sin embargo, las exponemos y procesamos bajo condiciones de relativa oscuridad. ¿Cuándo podemos dar más luz, en qué medida y por qué?
Impresión -- sensibilidad a la luz de hologramas blanqueados
Los hologramas de haluro de plata blanqueados son fotosensibles. ¿En qué medida? Diseñe algún experimento que sirva para comparar la sensibilidad de algún conjunto controlado de diferentes materiales, diferentes sustancias químicas de procesamiento, diferentes ambientes de almacenamiento o diferentes niveles de luz
Diseño de elementos ópticos holográficos
Los hologramas se pueden utilizar para reemplazar muchos de los elementos y dispositivos ópticos convencionales sencillos. En este proyecto se identificarían unos ejemplos y se realizaría una prueba inicial sobre uno o dos de estos hologramas.
Efectos de polarización en holografía
Sólo se grabará el componente del haz de referencia que es polarizado de la misma forma que el haz del objeto. Por lo tanto, la manipulación deliberada de la polarización del haz del objeto ofrece un interesante nivel de control que se puede explorar de muchas formas, como, por ejemplo, la eliminación de toques de luz, de reflexiones, de ruido imitación a la madera, etc.
Estudios de reflexión de colores falsos
El aumento de volumen de una emulsión holográfica previo a la exposición puede disminuir de forma significativa a la posterior reconstrucción. Por ejemplo, controlar este aumento infligiendo el agente dilatador en la placa, puede ofrecer un nuevo tipo de control creativo del medio, pero debe estar basado en precisos estudios de calibración previos.
Señal y ruido en los hologramas
No siempre es fácil cuantificar la luminosidad y el contraste de las imágenes holográficas, pero unos sencillos experimentos deberían revelar las dependencias básicas en la exposición y el ratio del haz, de los que hemos hablado.
Teoría tricolor
La reproducción de todos los colores por medio de la adición de los tres colores primarios es fundamental para el futuro de la holografía a color. Unas cuantas demostraciones deberían ser suficientes para aclarar algunos de los problemas de la interpretación del color en holografía. Es posible que se requiera la utilización de varios lásers diferentes, por lo que es mejor que se asegure de que puede disponer de ellos.
Estereogramas mínimos
Los estereogramas holográficos convencionales en dos pasos conllevan un proceso tan elaborado y que lleva tanto tiempo que se aleja del tipo de enfoque interactivo de "intente otra cosa esta vez", de gran importancia para una innovación de éxito. Es posible un enfoque mucho más simple en un sólo paso si el número de vistas en perspectiva se mantiene en un mínimo estricto, quizás incluso dos, como forma de "previsualizar" las consecuencias de un proceso más elaborado.
Fallo de reciprocidad en holografía
En principio, si se divide la exposición de un holograma en N partes igualmente incoherentes, la eficiencia de difracción de cada subholograma disminuye 1/n^2. En la práctica, hay un fuerte efecto como consecuencia de la clasificación de las exposiciones, denominado "fallo de reciprocidad". En el caso de los materiales y procesos empleados aquí, es necesario verificar estas observaciones.
Apilamiento en serie
Una forma de construir una imagen tridimensional a partir de una serie de secciones cruzadas es disponer dichas secciones en el espacio por medio de una serie de exposiciones múltiples. En este proyecto se explorarían los puntos fuertes y débiles de dicho método sencillo de apilamiento óptico de partes.
Reconocimiento de patrones
Se puede utilizar una variación de un holograma sencillo para "depurar" un documento por una palabra clave y producir puntos brillantes que correspondan a cada ubicación. Dicho proceso que se denomina "filtrado adaptado".
Adhesivos y tecnologías de soporte de objetos
Grabe los hologramas (de reflexión y de transmisión) realizados a partir de objetos precarios montados con diferentes adhesivos.
Ensayo de sensibilidad a la luz difusa y directa de la placa holográfica con lente colimadora y direccionadora
Conclusiones parciales. Luz difusa:
El desempeño de los HOES (hologramas) testeados para luz difusa en el cielo artificial fue muy pobre. No se visualizaron efectos significativos ya que la onda de luz al ser difusa proviene de varias direcciones. Si hubo algún efecto de redireccionamiento específico que fue tan leve que no logro ser detectado.
Mediciones con luz directa:
Con la aplicación de la luz directa de una lámpara de quarzt de 500 watt distanciada a 1 metro del HOE y la utilización de luxometros (fotómetros) se realizaron mediciones en 4 puntos en un arco de medición de 180 grados, tomados cada 5 grados y ubicados a una distancia de 0,50 m del HOE sobre papel negro. Las mediciones corresponden a cada uno de los HOE en las cuatro posiciones posibles de ambas caras. Se realiza un registro con maquina digital del comportamiento de cada uno de los HOES ante la aplicación de luz directa.
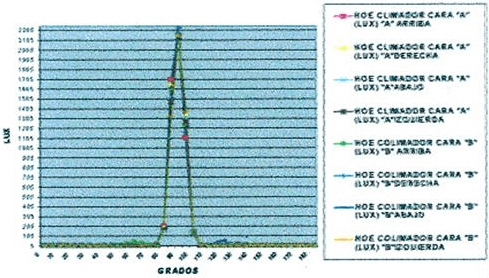
Comparación de resultados de lente colimadora holográfica
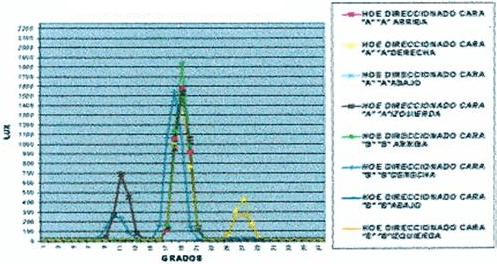
Comparación de resultados de lente direccionadora holográfica

Ensayo con luz directa blanca y luz difusa
Conclusiones parciales:
En la tabla 2 se puede observar que los resultados de las mediciones de ambas caras y en las cuatro posiciones son muy parejos, no hay variaciones considerables. La curva pronunciada que se observa en el sector medio del gráfico corresponde a luz directa que pasa a través de HOE. En este tipo de película holográfica no se produce una desviación de la luz con intensidad.
Autor: Guillermo Osvaldo Passera. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).