Tiro o lanzamiento parabólico
Se trata de un "movimiento rectilíneo uniforme" en su desarrollo horizontal y un "movimiento uniformemente variado" en su desarrollo vertical. En el eje vertical se comporta como el movimiento de "Tiro vertical".
Otro tipo de movimiento sencillo que se observa frecuentemente es el de una pelota que se lanza al aire formando un ángulo con la horizontal. Debido a la gravedad, la pelota experimenta una aceleración constante dirigida hacia abajo que primero reduce la velocidad vertical hacia arriba que tenía al principio y después aumenta su velocidad hacia abajo mientras cae hacia el suelo. Entretanto, la componente horizontal de la velocidad inicial permanece constante (si se prescinde de la resistencia del aire), lo que hace que la pelota se desplace a velocidad constante en dirección horizontal hasta que alcanza el suelo. Las componentes vertical y horizontal del movimiento son independientes, y se pueden analizar por separado. La trayectoria de la pelota resulta ser una parábola.
Es un movimiento cuya velocidad inicial tiene componentes en los ejes X e Y, en el eje Y se comporta como tiro vertical, mientras que en el eje X como MRU
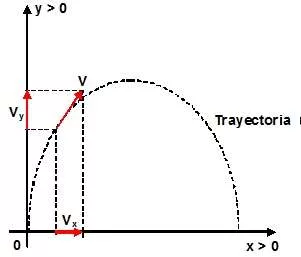
Gráfica del tiro parabólico
Características de las componentes según los ejes
| Eje | v | a |
| x | constante | 0 |
| y | 9,81 m/s² | g |
| Eje X (MRU) | Eje Y (MUV) | |||||
| 1) | v = Δx/t | Ecuación horaria de velocidad | 1) | yf = y0 + v0·t + ½·g·t² | Ecuación horaria de posición | |
| 2) | vf = v0 + g·t | Ecuación horaria de velocidad | ||||
| 3) | vf² = v0² + 2·g·Δy | |||||
Ecuaciones de la trayectoria
| Posición | x = (v0·cos θ0)·t y = (v0·sen θ0)·t - ½·g·t² |
| Velocidad | vx = v0·cos θ0 vy = v0·sen θ0 - g·t |
Altura máxima
Como se explicó anteriormente, el comportamiento en el eje Y es el característico del "Tiro vertical", por lo tanto, para el cálculo de la altura máxima se emplean las mismas ecuaciones.
1) yMáxima = y0 + v0·t + ½·g·t² (Ecuación horaria de posición)
2) 0 = v0 + g·t (Ecuación horaria de velocidad)
3) 0 = v0² + 2·g·Δy
Recordar que el valor de la aceleración de la gravedad depende del paralelo (latitud) en que se determine dicho valor. En el ecuador (latitud = 0) la aceleración es igual a "9,78049 m/s²", la aceleración promedio es de 9,81 m/s², es usual usar un valor de 10 m/s² para agilizar la resolución de ejercicios.
Ejemplo de tiro parabólico
Autor: Ricardo Santiago Netto. Argentina
¿Cuál es la aceleración de la gravedad? ¿Cuál es el sentido de la aceleración de la gravedad?