Impulso y cantidad de movimiento: colisiones
Colisiones
Durante un choque actúa una fuerza relativamente grande sobre las partículas que impactan, aunque solo lo hacen durante un intervalo de tiempo más o menos pequeño. Básicamente en una colisión el movimiento de las partículas que chocan (o, por lo menos, el de una de ellas) cambia en forma muy brusca y que podemos establecer una separación bastante definida entre los tiempos que transcurren "antes de la colisión" y los que lo hacen "después de ella".
Por ejemplo, cuando un bate golpea una pelota de béisbol, el principio y el fin de la colisión puede determinarse con muy buena precisión. El bate está en contacto con la pelota durante un intervalo de tiempo que es muy pequeño comparado con el tiempo en que la pelota esta en el aire. Durante la colisión el bate le aplica una gran fuerza a la pelota. Esta fuerza varía con el tiempo en una forma tan completa que solo puede medirse con dificultad. Tanto la pelota como el bate se desforman durante la colisión.
En las colisiones se verifica el principio de acción y reacción, es decir si el bate le aplica una fuerza a la pelota, la pelota reacciona con una fuerza de igual magnitud pero de sentido contrario, aunque en realidad es indistinto cual es la fuerza de acción y cual la de reacción, podemos decir si la pelota le aplica una fuerza al bate, el bate reacciona con una fuerza de igual magnitud pero de sentido contrario. En el caso de las colisiones estas fuerzas actúan durante lapso de tiempo muy pequeño y se denominan fuerzas instantáneas o impulsivas.
Cuando dos electrones "chocan" la fuerza que actúa entre ambos puede ser conocida fuerza electrostática de repulsión que está asociada con la carga de las partículas. Puede ser que las partículas no se toquen, pero aún así, podemos hablar de una colisión, porque una fuerza relativamente grande que actúa durante un tiempo que se considera pequeño comparado con el tiempo en que las partículas están en observación, tiene un gran efecto en el movimiento de los electrones.
Cuando un protón (H¹ o p) de 25 MeV de energía (1 MeV = 6,242·1012 J), "choca" con un núcleo de un isótopo de la plata (Ag107), las partículas pueden realmente "tocarse" ya que, en éste caso, la fuerza predominante que actúa entre ellas no es la fuerza electrostática repulsiva, si no la fuerza nuclear atractiva que es intensa y de corto alcance. El protón puede penetrar en el núcleo de la plata para formar una estructura compuesta, después de un tiempo pequeño -el "intervalo de la colisión" puede ser de 1018 segundos- la estructura compuesta puede separarse en dos partículas diferentes según un esquema tal como:
p + Ag107 ⟶ α + Pd104
En el que α = He4 es una partícula alfa. En consecuencia el concepto de colisión puede aplicarse para que incluya eventos (que generalmente se llaman reacciones) en los que cambian las identidades de las partículas que interaccionan. Los principios de conservación son aplicables a todos estos ejemplos.
Si se desea, la definición de una colisión puede ampliarse aún más para incluir en ella a la desintegración espontánea de una partícula en dos o más partículas distintas. Un ejemplo de esto es la desintegración de una partícula elemental, llamada la partícula sigma, en otras dos partículas, el pión y el neutrón según el esquema:
∑ ⟶ π¯ + n
Aunque en éste proceso no ocurre que dos cuerpos lleguen a estar en contacto (a menos que se le considere en sentido inverso) tiene muchas características en común con las colisiones, a saber:
1 - Hay una distinción clara entre "antes del suceso" y "después de suceso".
2 - Las leyes de la conservación del ímpetu y de la energía proporcionan mucha información relacionada con éste tipo de proceso, estudiando las situaciones "antes" y "después", aún cuando se sepa poco sobre las leyes de las fuerzas que operan durante el "evento" mismo.
El Impulso y la Cantidad de Movimiento
Supongamos que la figura 1 muestra la magnitud de la fuerza ejercida sobre un cuerpo durante una colisión. También supongamos que dicha fuerza tiene una dirección constante. La colisión comienza en el instante ti y termina en el tf, y la fuerza es nula antes y después del choque. El cambio de la cantidad de movimiento o ímpetu dp de un cuerpo, en el intervalo de tiempo dt durante el cual ha estado actuando una fuerza F sobre él puede escribirse como:
dp = F·dt
El cambio en la cantidad de movimiento del cuerpo durante una colisión, puede obtenerse integrando sobre el tiempo que dura dicha colisión, es decir:
| Δp = pf - pi = ∫ | pf | dp = ∫ | tf | dt |
| pi | ti |
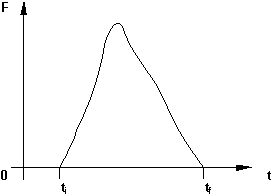
Gráfico de la variación de una fuerza durante una colisión
Figura 1: La figura muestra como puede variar con el tiempo una fuerza instantánea durante una colisión que comienza en el tiempo ti y finaliza en el timpo tf.
La integral de una fuerza sobre el intervalo de tiempo en que actúa se llama impulso I de la fuerza. Por lo tanto el cambio de la cantidad de movimiento p de un cuerpo movido por una fuerza impulsiva, es igual al impulso. Tanto el impulso como la cantidad de movimiento son vectores y ambos tienen las mismas unidades y dimensiones.
Para el impulso:
I = F·t
Siendo:
I: impulso (kg·m/s)
Para la cantidad de movimiento:
p = m·v
Siendo:
p: cantidad de movimiento (kg·m/s)
Conservación de la Cantidad de Movimiento Durante las Colisiones
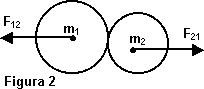
Esquema de las fuerzas actuantes sobre las masas en una colisión
Considerando ahora una colisión entre dos partículas, tales como las de las masa m1 y m2 (figura 2), durante la breve colisión, las partículas ejercen fuerzas internas entre sí. En cualquier instante F12 es la fuerza ejercida la partícula 2 sobre la partícula 1 y F21 es la fuerza ejercida por la partícula 1 sobre la partícula 2. Por la tercera ley de Newton, estas fuerzas son, en cualquier instante, de igual magnitud pero de sentido contrario (acción y reacción).
El cambio de la cantidad de movimiento de la partícula 1 como resultado del choque es:
| Δp1 = ∫ | tf | F1,2·dt = F1,2,m·Δt |
| ti |
En donde F1,2,m es el valor medio de la fuerza durante el intervalo de tiempo Δt = tf - ti que dura la colisión.
El cambio de la cantidad de movimiento de la partícula 2 como resultado del choque es:
| Δp2 = ∫ | tf | F2,1·dt = F2,1,m·Δt |
| ti |
En donde F2,1,m es el valor medio de la fuerza durante el intervalo de tiempo Δt = tf - ti que dura la colisión.
Si sobre las partículas no actúan otras fuerza, el cambio total en la cantidad de movimiento de cada una de ellas es Δp1 y Δp2. Pero hemos visto que en cada instante, F12 = -F21, de modo que F12m = -F21m y, por lo tanto:
Δp1 = -Δp2
Si consideramos que las dos partículas forman un sistema aislado, la cantidad de movimiento total del sistema es:
p = p1 + p2
Y el cambio total en la cantidad de movimiento del sistema provocado por la colisión es cero, o sea que:
Δp = p1 + p2 = 0
Por lo tanto si no hay fuerzas externas, la colisión no altera la cantidad de movimiento total del sistema. Las fuerzas impulsivas que actúan durante la colisión son fuerzas internas que no producen ningún efecto sobre la cantidad de movimiento total del sistema.
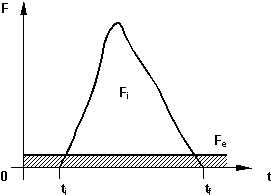
Gráfico de las fuerzas impulsivas y externas durante una colisión
Figura 3: Durante la colisión la fuerza impulsiva Fi es generalmente mucho mayor que cualquiera de la fuerzas externas Fe que pueden estar actuando sobre el sistema.
Se ha definido un choque como una interacción que tiene lugar en un tiempo Δ que es despreciable comparado con el tiempo durante el cual se observa el sistema. También podemos caracterizar a una colisión como un suceso en el que las fuerzas externas que pueden estar actuando sobre el sistema sean despreciables comparadas con las fuerzas impulsivas de la colisión.
Cuando un bate golpea a una pelota de béisbol también actúan fuerzas externas sobre el sistema, por ejemplo la gravedad o la fuerza rozamiento del aire. Estas fuerzas externas pueden no ser las mismas para todos los cuerpos que intervengan en la colisión ni tienen que ser necesariamente equilibradas por otras fuerzas externas. Aún así las fuerzas externas pueden ignorarse, sin mucho riesgo, durante la colisión y se puede suponer la validez de la conservación de la cantidad de movimiento, ya que, como sucede casi siempre, las fuerzas externas son despreciables comparadas con las fuerzas impulsivas de la colisión. De esto resulta que durante una colisión, el cambio en la cantidad de movimiento de una partícula, proveniente de una fuerza externa, es despreciable comparado con el cambio en la cantidad de movimiento de dicha partícula debido a la fuerza impulsiva de la colisión (figura 3).
Por ejemplo, cuando un bate golpea a una pelota de béisbol, la colisión solo dura una pequeña fracción de segundo. Como el cambio en la cantidad de movimiento es grande y el tiempo de la colisión es pequeño, resulta que la fuerza impulsiva promedio Fm es relativamente grande, comparada con ésta, la fuerza de la gravedad es despreciable. Al determina el cambio del movimiento de la pelota, durante la colisión, podemos ignorar, sin riesgo alguno, a esta fuerza externa. Mientras menor sea la duración del choque mejor será el resultado obtenido.
Por lo tanto, en la práctica podemos aplicar el principio de la conservación de la cantidad de movimiento durante las colisiones, con tal de que el tiempo que dura la colisión sea suficientemente pequeño. Entonces podemos decir que la cantidad de movimiento de un sistema de partículas justo antes de que choquen, es igual a la cantidad de movimiento del sistema inmediatamente después de que ello ocurra.
Bibliografía:
Física - Robert Resnick David Holliday
Autor: Ricardo Santiago Netto. Argentina.
- ‹ Anterior
- |
- Siguiente ›
Relación entre impulso y cantidad de movimiento. ¿Qué es el impulso y la cantidad de movimiento? ¿Qué diferencia hay entre colisiones elásticas e inelásticas o plásticas?