Movimiento circular uniforme en el plano

El movimiento circular es otro tipo de movimiento sencillo. Si un objeto se mueve con celeridad constante pero la aceleración forma siempre un ángulo recto con su velocidad, se desplazará en un círculo. La aceleración está dirigida hacia el centro del círculo y se denomina aceleración normal o centrípeta. En el caso de un objeto que se desplaza a velocidad v en un círculo de radio r, la aceleración centrípeta es:

a = v²/r

En este movimiento, tanto la aceleración como la velocidad tienen componentes en x e y.

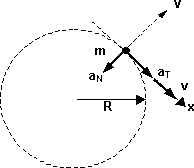
Representación gráfica de las velocidades y aceleraciones en un movimiento circular

1) Movimiento circular uniforme horizontal:

Arco de circunferencia recorrido (s)

s = R·θ

[s] = (m)

θ: ángulo desplazado

R: radio de la circunferencia [R] = (m)

Velocidad tangencial (v)

v = R·ω

[v] = (m/s)

ω: velocidad angular [ω] = (s⁻¹)

T: período (tiempo que demora en recorrer una vuelta completa) [T] = (s)

Frecuencia (f)

[f] = (s⁻¹) o (Hz) o (RPM)

Frecuencia en función de la velocidad angular

Velocidad angular (ω)

De frecuencia en RPM a velocidad angular:

Relación entre la velocidad angular y la tangencial a igual período:

Ecuación horaria de velocidad angular:

ω₂ = ω₁ ± α·t

Aceleración tangencial (a_T)

a_T = R·α

[a_T] = (m/s²)

α: aceleración angular

Aceleración normal o centrípeta (a_N)

a_N = R·ω²

a_N = v·ω

[a_N] = (m/s²)

Sí v = constante ⇒ a_T = 0

Aceleración angular en función de la velocidad tangencial el tiempo y el radio (α)

Aceleración angular en función de la velocidad tangencial el tiempo y el radio (α)

Ejemplo del movimiento circular uniforme horizontal

Fuerza

Aplicando los conceptos de la dinámica, si en el movimiento hay aceleración, habrá fuerza.

Fuerza centrípeta (F_N)

Fuerza centrífuga (F_C)

Por el principio de acción y reacción, sabemos que esa fuerza centrípeta origina una reacción y opuesta que es la fuerza centrífuga.

2) Movimiento circular uniforme vertical:

Este movimiento no es uniforme ya que la velocidad del cuerpo aumenta cuando desciende y disminuye cuando asciende. Para este modelo el cuerpo está sujeto por una cuerda, entonces, las fuerzas que actúan son el peso del cuerpo y la tensión de la cuerda, que componen una fuerza resultante.

F_T = m·g·sen θ

F_N = T - m·g·cos θ

T = m·(v²/R + g·cos θ)

Siendo en el punto más bajo

T = m·(v²/R + g)

Siendo en el punto más alto

T = m·(v²/R - g)

En el punto más alto la velocidad es crítica, por debajo de ésta la cuerda deja de estar tensa.

v_c² = R·g

Rueda trasera de la bicicleta: ejemplo del movimiento circular uniforme vertical

Bibliografía:

"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.

"Física Universitaria". Sears, Zemansky, Young. España.

Autor: Ricardo Santiago Netto. Argentina