Problema nº 2 de dinámica de los fluidos, alcance de un chorro de agua - TP05
Enunciado del ejercicio nº 2
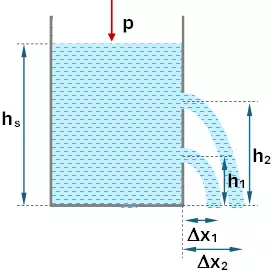
En la pared lateral de un recipiente lleno de líquido hasta 90 cm de altura, se abren dos orificios a 15 cm y 60 cm sobre el fondo. Calcular el alcance de ambos chorros en el instante inicial.
Desarrollo
Datos:
h₁ = 15 cm
h₂ = 60 cm
hₜ = 90 cm
g = 9,81 m/s²
Fórmulas:
p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂
h = ½·g·t²
| vₓ = v = | Δx |
| t |
Esquema:
Solución
Para resolver el ejercicios con los datos dados, primero debemos hallar la velocidad de salida por cada orificio.
Aplicamos la ecuación de Bernoulli para flujo ideal sin fricción.
p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂
El enunciado dice "superficie libre del líquido" por lo tanto:
p₁ = p₂ = presión atmosférica
½·δ·v₁² + δ·g·h₁ = ½·δ·v₂² + δ·g·h₂
Y la velocidad en la superficie del líquido se considera nula:
v₂ = 0
½·δ·v₁² + δ·g·h₁ = δ·g·h₂
La densidad se simplifica:
½·v₁² + g·h₁ = g·h₂
Despejamos la velocidad:
½·v₁² = g·h₂ - g·h₁
½·v₁² = g·(h₂ - h₁)
v₁² = 2·g·(h₂ - h₁)
v₁ = √2·g·(h₂ - h₁)
Calculamos la velocidad para cada orificio, es decir, v₁ y v₁
v₁ = √2·g·(hₜ - h₁)
v₂ = √2·g·(hₜ - h₂)
Convertimos las unidades:
| h₁ = 15 cm· | 1 m |
| 100 cm |
h₁ = 0,15 m
| h₂ = 60 cm· | 1 m |
| 100 cm |
h₂ = 0,60 m
| hₜ = 90 cm· | 1 m |
| 100 cm |
hₜ = 0,90 m
Reemplazamos y calculamos:
v₁ = √2·9,81 m/s²·(0,90 m - 0,15 m)
v₁ = √19,62 m/s²·0,75 m
v₁ = √14,715 m²/s²
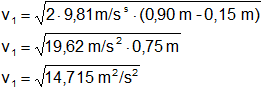
v₁ = 3,836013556 m/s
v₂ = √2·9,81 m/s²·(0,90 m - 0,60 m)
v₂ = √19,62 m/s²·0,30 m
v₂ = √5,886 m²/s²
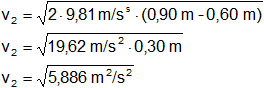
v₂ = 2,426107994 m/s
Con los datos hallados de las velocidades podemos calcular el tiempo.
A partir de que el agua sale por cada orificio el chorro de agua describe un movimiento de tiro oblicuo.
En el eje "Y" su velocidad inicial es nula y su aceleración es la de la gravedad.
En el eje "X" su velocidad es constante y su valor el hallado en el ítem anterior.
Las ecuaciones de cinemática para este caso son:
h = ½·g·t²
| vₓ = v = | Δx |
| t |
De la primera ecuación despejamos el tiempo "t" que necesitamos para resolver la segunda ecuación:
| t₁² = | 2·h₁ |
| g |
| t₂² = | 2·h₂ |
| g |
Reemplazamos y calculamos:
| t₁² = | 2·0,15 m |
| 9,81 m/s² |
| t₁² = | 0,30 s² |
| 9,81 |
t₁ = √0,03058104 s²
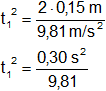
t₁ = 0,174874354 s
| t₂² = | 2·0,60 m |
| 9,81 m/s² |
| t₂² = | 1,20 s² |
| 9,81 |
t₂ = √0,122324159 s²
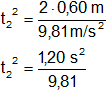
t₂ = 0,349748708 s
De la segunda ecuación despejamos "Δx" y reemplazamos el valor del tiempo hallado:
| vₓ = | Δx |
| t |
Δx₁ = v₁ₓ·t₁
Δx₁ = 3,836013556 m/s·0,174874354 s
Δx₁ = 0,670820393 m
Δx₂ = v₂ₓ·t₂
Δx₂ = 2,426107994 m/s·0,349748708 s
Δx₂ = 0,848528137 m
Resultado, el alcance de cada chorro es:
Δx₁ = 0,67 m
Δx₂ = 0,85 m
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular el alcance de un chorro de agua