Problema nº 8 de dinámica de los fluidos, caudal de un corriente estacionaria - TP05
Enunciado del ejercicio nº 8
El área de la sección transversal de una tubería horizontal por la que circula agua es de 10 cm². En otro tramo, el área de la sección transversal es de 5 cm². La diferencia de presiones entre ambas secciones es de 300 Pa. ¿Cuántos metros cúbicos de agua saldrán de la tubería en 1 minuto?
Desarrollo
Datos:
Δp = 300 Pa
A₁ = 10 cm²
A₂ = 5 cm²
δ = 1.000 kg/m³
Fórmulas:
Q = v·A
p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂
Esquema:

Solución
Aplicamos la ecuación de Bernoulli para flujo ideal sin fricción.
p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂
p₂ - p₁ = ½·δ·v₁² + δ·g·h₁ - (½·δ·v₂² + δ·g·h₂)
p₂ - p₁ = ½·δ·v₁² + δ·g·h₁ - ½·δ·v₂² - δ·g·h₂
No hay diferencia de altura, por lo tanto:
h₁ = h₁ = 0
p₂ - p₁ = ½·δ·v₁² - ½·δ·v₂²
p₂ - p₁ = ½·δ·(v₁² - v₂²)
Δp = p₂ - p₁ (p₂ < p₁ ⇒ Δp < 0)
Δp = -300 Pa
Δp = ½·δ·(v₁² - v₂²)
![]() (1)
(1)
De la ecuación de continuidad sabemos que:
Q = v₁·A₁ = v₂·A₂ = constante
v₁·A₁ = v₂·A₂
Despejamos v₂:
![]()
Reemplazamos por los valores:
![]()
Tenemos la relación entre las velocidades:
v₂ = 2·v₁
Reemplazamos en la ecuación (1):
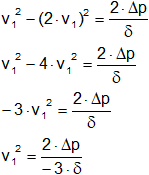
Reemplazamos por los valores y calculamos:

v₁ = 0,447213595 m/s
Convertimos las unidades de superficie:
![]()
A₁ = 0,001 m²
Aplicamos la ecuación de continuidad en el punto "1":
Q = v₁·A₁
Reemplazamos por los datos y calculamos:
Q = 0,447213595 m/s·0,001 m²
Q = 0,000447214 m³/s
Pide el resultado en m³/min, convertimos las unidades:
![]()
Q = 0,0268328 m³/min
Resultado, el caudal es:
Q = 0,0268 m³/min
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular el caudal de un corriente estacionaria.