Ejemplo n° 2 de movimiento de planetas y satélites

Ejemplo nº 2

Calcula la velocidad orbital y la altura sobre el ecuador a la que debe situarse un satélite geoestacionario.

Un satélite geoestacionario debe tener un período de revolución igual a la rotación de la Tierra alrededor de su propio eje.

Desarrollo

Datos:

T = 24 h = 86.400 s.

Fórmulas:

Solución

Aplicamos las ecuaciones de la velocidad orbital y del período de revolución para obtener un sistema de dos ecuaciones con dos incógnitas:

Al despejar r de la segunda ecuación y sustituirla en la primera, obtenemos:

Calculamos la velocidad orbital:

Resultado, la velocidad orbital del satélite geoestacionario es:

v = 3,1·10³ m/s

Primero debemos hallar el radio de la órbita para calcular la altura a la superficie de la Tierra, h:

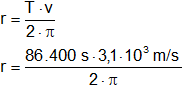
r = 4,26·10⁷ m

Finalmente, despejamos h de la expresión:

r = R_T + h

Sustituimos los datos:

h = r - R_T

h = 4,26·10⁷ m - 6,37·10⁶ m

Resultado, la altura sobre el ecuador a la que debe situarse un satélite geoestacionario es:

h = 3,62·10⁷ m

‹‹ Regresar al apunte: AP15

• Fuente:

Física de 2° de Bachillerato - Colegio Montpellier

Autor: Leandro Bautista. España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

Ejemplo, cómo calcular la velocidad orbital de un satélite.