Problema nº 3 de dinámica, fuerza gravitatoria en un satélite - TP07
Enunciado del ejercicio nº 3
Un satélite de comunicaciones de 200 kg de masa se encuentra en una órbita circular de 40.000 km de radio alrededor de la Tierra (la masa de la Tierra es 5,97·10²⁴ kg). ¿Cuál es la fuerza gravitatoria sobre el satélite?
Desarrollo
Datos:
mS = 200 kg
mT = 5,97·10²⁴ kg
r = 40.000 km
G = 6,67·10⁻¹¹ N·m²/kg²
Fórmulas:
![]()
Solución
La cuarta ley de Newton dice que la fuerza (Fg) de atracción entre dos masas depende de la distancia entre ellas y de la constante de universal de la gravitación G. Se expresa:
![]()
Convertimos las unidades de longitud:
![]()
r = 40.000.000 m = 4·10⁷ m
Reemplazamos por los datos y calculamos:
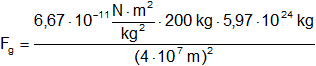
Sumamos los exponentes de igual base y simplificamos las unidades:
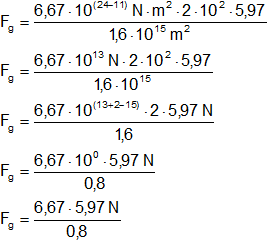
Fg = 49,774875 N
Resultado, la fuerza gravitatoria sobre el satélite es:
Fg = 49,77 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP07
- | Siguiente ›
Ejemplo, cómo calcular la fuerza de la gravedad en un satélite.