Ejemplo n° 8 de inducción electromagnética
Ejemplo nº 8
Un alternador consta de una bobina de 40 espiras cuadradas de 5 cm de lado y una resistencia total de 16 Ω. La bobina gira con una frecuencia de 100 Hz en un campo magnético constante de 0,8 T. Determina:
a) La fuerza electromotriz máxima que se induce.
b) El valor máximo de la intensidad inducida.
c) Una expresión para la fuerza electromotriz y la intensidad inducida en función del tiempo. Traza las respectivas gráficas de estas dos magnitudes.
Desarrollo
Datos:
N = 40
l = 5 cm = 0,05 m
R = 16 Ω
f = 100 Hz
B = 0,8 T
Fórmulas:
εinducida = N·B·S·ω·sen ω·τ
![]()
Solución
a)
La fuerza electromotriz inducida viene dada por la expresión:
εinducida = N·B·S·ω·sen ω·τ
Donde:
s = 2,5·10⁻³ m²
ω = 2·π·f = 200·π = 628 rad/s
Por lo tanto, la fuerza electromotriz inducida es máxima cuando sen ω·τ = 1 y valdrá:
ε₀ = N·B·S·ω = 40·0,8·T·2,5·10⁻³ m²·628 rad/s
ε₀ = 50,24 V
b)
Puesto que la resistencia total de la bobina es de 16 Ω, la intensidad inducida máxima valdrá:
![]()
Reemplazamos por los valores y calculamos:
![]()
I₀ = 3,14 A
c)
Las expresiones para la fuerza electromotriz y la intensidad inducidas son, respectivamente:
ε = 50,24·sen 200·π·τ V
i = 3,14·sen 200·π·τ A
Las representaciones gráficas pueden verse en las siguientes figuras:
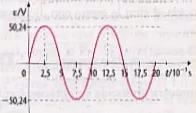
Gráfico de la fem en función del tiempo
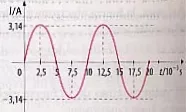
Gráfico de la corriente inducida en función del tiempo
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Ejemplo, cómo determinar la corriente inducida