Sistemas eléctricos e instrumentación
Resistencia.
| iR(t) = | 1 | vR(t) | L ⟶ | IR(s) = | 1 | VR |
| R | R |
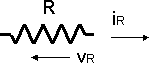
Inductancia.
| iL(t) = | 1 | ∫vL(t)·dt | L ⟶ | IL(s) = | 1 | VL |
| L | sL |
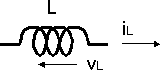
Capacitancia.
| iC(t) = C· | dvC(t) | L ⟶ | IC(s) = sC·VC |
| dt |
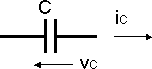
Ejemplo nº 1
Encontrar la transferencia V₂(s)/I₁(s)
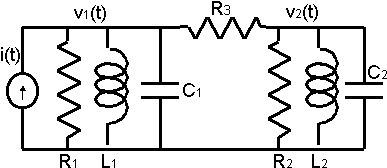
Circuito eléctrico con capacitor, resistencia e inductancia
Nodo 1:
| i₁(t) = C₁· | dv₁(t) | + | v₁(t) | + | v₁(t) | + | 1 | ·∫v₁(t)·dt - | v₂(t) |
| dt | R₁ | R₃ | L₁ | R₃ |
| ∴ ⟶ i₁(s) = (C₁s + | 1 | + | 1 | + | 1 | )·V₁(s) - | v₂(2) |
| R₁ | R₃ | sL₁ | R₃ |
Nodo 2:
| 0 = - | v₁(t) | + C₂· | dv₂(t) | + | v₂(t) | + | v₂(t) | + | 1 | ·∫v₂(t)·dt |
| R₃ | dt | R₂ | R₃ | L₂ |
| ∴ ⟶ 0 = - | v₁(t) | + (C₂s + | 1 | + | 1 | + | 1 | )·V₂(s) |
| R₃ | R₂ | R₃ | sL₂ |
V₂(s)/I₁(s) =
Sistemas mecánicos traslacionales
Ejemplo nº 2
Encontrar la transferencia Xₐ(s)/F(s)
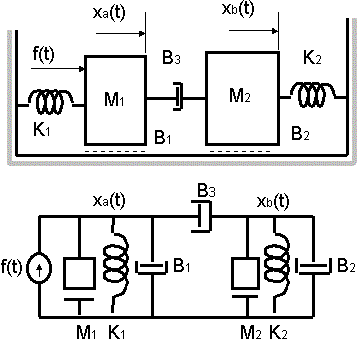
Circuito de un sistema mecánico traslacional
Nodo a ⟶ F(s) = (M₁·s² + B₁·s + B₃·s + K₁)·Xₐ(s) - B₃·s·Xb(s)
Nodo b ⟶ 0 = -B₃·s·Xₐ(s) + (M₂·s² + B₂·s + B₃·s + K₂)·Xb(s)
Xₐ(s)/F(s)
Sistemas mecánicos rotacionales
Ejemplo nº 3
Encontrar la transferencia θ₂(s)/T(s)
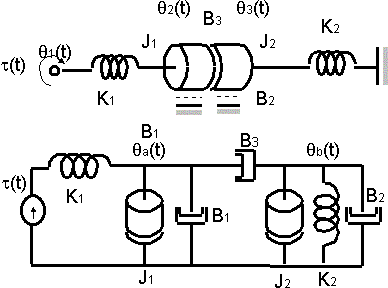
Circuito de un sistema mecánico rotacional
Nodo θ₁ ⟶ T(s) = K₁·θ₁(s) - K₁ θ₂(s)
Nodo θ₂ ⟶ 0 = -K₁·θ₁(s) + (J₁·s² + B₁·s + B₃·s + K₁) θ₂(s) - B₃·s θ₃(s)
Nodo θ₃ ⟶ 0 = -B₃·s θ₂(s) + (J₂·s² + B₂·s + B₃·s + K₂) θ₃(s)
Θ₂(s)/T(s)
Sistemas térmicos
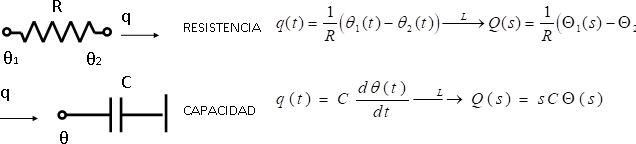
Ejemplo: Termómetro clínico
RG = R vidrio-aire
RM = R mercurio-vidrio
CG = C vidrio
CM = C mercurio
Encontrar: ΘM(s)/Θ₀(s)
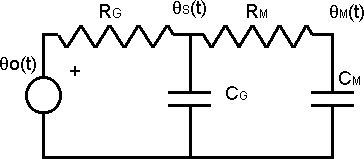
Circuito de un sistema térmico
Nodo: S
| 0 = - | Θ₀(s) | - | ΘM(s) | + ( | 1 | + | 1 | + sCG)·Θₛ(s) |
| RG | RM | RG | RM |
Nodo: M
| 0 = - | Θₛ(s) | + ( | 1 | + sCM)·ΘM(s) |
| RM | RM |
ΘM(s)/Θ₀(s)
Sistemas hidráulicos
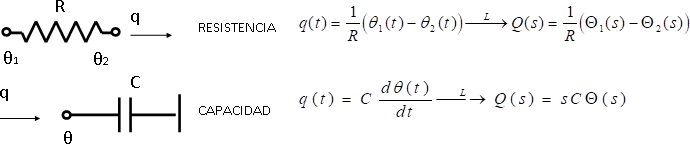
Nodo: 1
| Qᵢ(s) = ( | 1 | + sA₁)·H₁(s) - | H₂(s) |
| R₁ | R₁ |
Nodo: 2
| 0 = - | H₁(s) | + ( | 1 | + | 1 | + sA₂)·H₂(s) |
| R₁ | R₁ | R₂ |
H₁(s)/Q₁(s)
Sistemas neumáticos
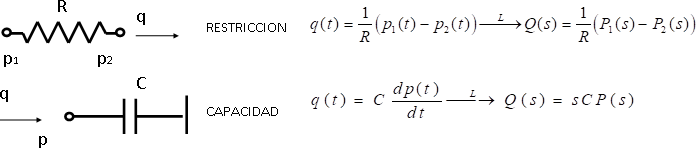
A volumen y temperatura constante:
| C = dm/dp q(t) = dm/dt | ∴q(t) = C·dp/dt ⟶ |
| dm | = | d(V·δ) | = V· | dδ |
| dp | dp | dp |
p·v = R·T ⟶ p/δ = R·T
| dδ | = | 1 |
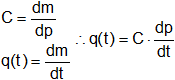
| dp | R·T |
| ∴ C = | V |
| R·T |
Ejemplo nº 4
Hallar la transferencia: P₁(s)/P₀(s)
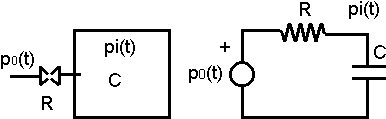
Circuito de un sistema neumático
En el nodo p1:
0 = -R·p₀(t) + R·p₁(t) + C·p₁(t) ∴
0 = -R·P₀(s) + R·P₁(s) + sC·P₁(s) ∴
R·P₀(s) = P₁(s)·(R + sC) ∴
| P₁(s) | = | R | = | 1 |
| P₀(s) | R + sC | 1 + sC·R |
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).