Problema nº 4 de resultante y resta de fuerzas concurrentes - TP04
Enunciado del ejercicio nº 4
Dos fuerzas F₁ y F₂ actúan sobre un punto, F₁ es de 8 N y su dirección forma un ángulo de 60° por encima del eje X en el primer cuadrante, F₂ es de 5 N y su dirección forma un ángulo de 53° por debajo del eje X en el cuarto cuadrante, determinar:
a) Las componentes de la resultante.
b) La magnitud de la resultante.
c) La magnitud de la diferencia F₁ - F₂
Desarrollo
Datos:
F₁ = 8 N
F₂ = 5 N
α = 60°
β = 53°
Solución
Las fuerzas concurrentes son aquellas cuyas sus rectas de acción concurren en un punto o, lo que es igual, tienen un punto en común.
Primero realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes como indica el enunciado.
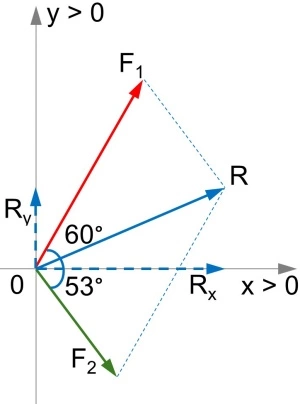
a) Hallamos las componentes de la resultante.
La resultante (en el eje "x") será:
Rₓ = F₁ₓ + F₂ₓ (1)
La resultante (en el eje "y") será:
Ry = F1y - F2y (2)
Por trigonometría sabemos que:
| cos 60° = | F₁ₓ |
| F₁ |
F₁ₓ = F₁·cos 60°
| sen 60° = | F1y |
| F₁ |
F1y = F₁·sen 60°
| cos 53° = | F₂ₓ |
| F₂ |
F₂ₓ = F₂·cos 53°
| sen 53° = | F2y |
| F₂ |
F2y = F₂·sen 53°
Reemplazamos en las ecuaciones (1) y (2):
Rₓ = F₁·cos 60° + F₂·cos 53°
Ry = F₁·sen 60° - F₂·sen 53°
Reemplazamos por los valores y calculamos:
Rₓ = 8 N·cos 60° + 5 N·cos 53°
Rₓ = 8 N·0,5 + 5 N·0,601815023
Rₓ = 4 N + 3,009075116 N
Rₓ = 7,009075116 N
Ry = 8 N·sen 60° - 5 N·sen 53°
Ry = 8 N·0,866025404 - 5 N·0,79863551
Ry = 6,92820323 N - 3,99317755 N
Ry = 2,93502568 N
Resultado a), las componentes de la resultante son:
Rₓ = 7,01 N
Ry = 2,94 N
b) Cálculo de la magnitud de la resultante.
Aplicamos el teorema de Pitágoras con los valores hallados de las componentes:
R² = Rₓ² + Ry²
Reemplazamos por los valores y calculamos:
R² = (7,01 N)² + (2,94 N)²
R² = 49,12713398 N² + 8,614375742 N²
R² = 57,74150972 N²
R = √57,74150972 N²
R = 7,598783437 N
Resultado b), el módulo de la resultante es:
R = 7,6 N
c) Cálculo de la magnitud de la diferencia F₁ - F₂.
Si R es la resultante de la suma, llamamos S a la resultante de la resta:
S = F₁ - F₂
S² = Sₓ² + Sy²
Recurrimos a las ecuaciones (1) y (2) pasa S:
Sₓ = F₁·cos 60° - F₂·cos 53°
Sy = F₁·sen 60° - (-F₂·sen 53°)
Reemplazamos por los valores y calculamos:
Sₓ = 8 N·cos 60° - 5 N·cos 53°
Sₓ = 8 N·0,5 - 5 N·0,601815023
Sₓ = 4 N - 3,009075116 N
Sₓ = 0,990924884 N
Sy = 8 N·sen 60° + 5 N·sen 53°
Sy = 8 N·0,866025404 + 5 N·0,79863551
Sy = 6,92820323 N + 3,99317755 N
Sy = 10,92138078 N
Aplicamos el teorema de Pitágoras:
S² = Sₓ² + Sy²
S² = (0,990924884 N)² + (10,92138078 N)²
S² = 0,981932126 N² + 119,2765582 N²
S² = 120,2584903 N²
S = √120,2584903 N²
S = 10,96624322 N
Resultado c), el valor de F₁ - F₂ es:
S = 11 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo calcular la resultante de un sistema de fuerzas concurrentes. Problemas de estática resueltos y fáciles.