Problema nº 8 de condición de equilibrio. Cuerpos suspendidos y fuerza elástica - TP09

Enunciado del ejercicio nº 8

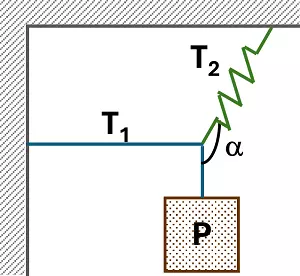
Se tiene un bloque de peso desconocido colgado en la forma que muestra la figura. La cuerda 2 posee un resorte que se ha estirado 10 cm, si su constante es k = 100.000 gf/cm, averiguar el valor de la masa del bloque y T₁ (α = 150°).

Desarrollo

Datos:

k = 100.000 gf/cm

x = 10 cm

α = 150°

Fórmulas:

Condición de equilibrio (Primera ley de Newton):

∑Fₓ = 0

∑F_y = 0

F = k·x

Esquema:

Solución

Primero realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes convenientemente.

Descomponemos la tensión T₂ en sus componentes sobre los ejes:

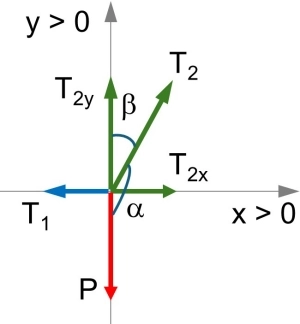
Planteamos las ecuaciones para que el sistema cumpla las condiciones de equilibrio.

En el eje X las fuerzas son:

T₂ₓ - T₁ = 0 (1)

En el eje Y las fuerzas son:

T_2y - P = 0 (2)

Luego:

β = 180° - α

β = 180° - 150°

β = 30°

Por trigonometría sabemos que:

T₂ₓ = T₂·sen β

T_2y = T₂·cos β

T₂ se calcula con la fórmula de la fuerza elástica:

T₂ = k·x

Adecuamos las unidades:

k = 10.000 kgf/m

x = 0,1 m

Reemplazamos en (2):

T_2y - P = 0

T₂·cos β - P = 0

k·x·cos β - P = 0

Despejamos P:

P = k·x·cos β

Reemplazamos por los valores y calculamos:

P = 10.000 kgf/m·0,1 m·cos 30°

P = 1.000 kgf·0,866025404

P = 866,0254038 kgf

Resultado, el valor de la fuerza peso es:

P = 866,0254038 kgf

Luego reemplazamos en (1):

T₂ₓ - T₁ = 0

T₂·sen β - T₁ = 0

k·x·sen β - T₁ = 0

Despejamos T₁:

k·x·sen β = T₁

Reemplazamos por los valores y calculamos:

T₁ = 10.000 kgf/m·0,1 m·sen 30°

T₁ = 1.000 kgf·0,5

T₁ = 500 kgf

Resultado, el valor de la tensión T₁ es:

T₁ = 500 kgf

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP09
• | Siguiente ›

Ejemplo, cómo calcular la tensión y el peso de un cuerpo suspendido. Problemas de estática resueltos y fáciles.