El sonido y las ondas: Fenómenos ondulatorios

Fenómenos ondulatorios

Las propiedades de las ondas se manifiestan a través de una serie de fenómenos que constituyen lo esencial del comportamiento ondulatorio. Así, las ondas rebotan ante una barrera, cambian de dirección cuando pasan de un medio a otro, suman sus efectos de una forma muy especial y pueden salvar obstáculos o bordear las esquinas.

El estudio de los fenómenos ondulatorios supone la utilización de conceptos tales como período, frecuencia, longitud de onda y amplitud, y junto a ellos el de frente de onda, el cual es característico de las ondas bi y tridimensionales.

Se denomina frente de ondas al lugar geométrico de los puntos del medio que son alcanzados en un mismo instante por la perturbación.

Las ondas que se producen en la superficie de un lago, como consecuencia de una vibración producida en uno de sus puntos, poseen frentes de onda circulares. Cada uno de esos frentes se corresponden con un conjunto de puntos del medio que están en el mismo estado de vibración, es decir a igual altura. Debido a que las propiedades del medio, tales como densidad o elasticidad, son las mismas en todas las direcciones, la perturbación avanza desde el foco a igual velocidad a lo largo de cada una de ellas, lo que explica la forma circular y, por tanto, equidistante del foco, de esa línea que contiene a los puntos que se encuentran en el mismo estado de vibración.

Las ondas tridimensionales, como las producidas por un globo esférico que se infla y desinfla alternativamente, poseen frentes de ondas esféricos si el foco es puntual y si el medio, como en el caso anterior, es homogéneo.

El principio de Huygens

La explicación de los fenómenos ondulatorios puede hacerse de forma sencilla sobre la base de un principio propuesto por Christiaan Huygens (1.629 - 1.695) para ondas luminosas, pero que es aplicable a cualquier tipo de ondas. La observación de que las ondas en la superficie del agua se propagaran de una forma gradual y progresiva suscitó en Huygens la idea de que la perturbación en un instante posterior debería ser producida por la perturbación en otro anterior. Este fue el germen del siguiente principio general de propagación de las ondas que lleva su nombre:

« Cada uno de los puntos de un frente de ondas puede ser considerado como un nuevo foco emisor de ondas secundarias que avanzan en el sentido de la perturbación y cuya envolvente en un instante posterior constituye el nuevo frente ».

La aplicación del principio de Huygens se lleva a efecto mediante un método puramente geométrico conocido como método de construcción de Huygens. En el caso de una onda bidimensional circular producida por un foco o fuente puntual la aplicación de este método sería como sigue.

Si S es el frente de ondas correspondiente a un instante cualquiera t, según el principio de Huygens, cada punto de S se comporta como un emisor de ondas secundarias también circulares. Al cabo de un intervalo de tiempo t los nuevos frentes formarán una familia de circunferencias Si, con sus centros situados en cada uno de los puntos de Sy cuyo radio r = v·Δt será el mismo para todas ellas si la velocidad v de propagación es igual en cualquier dirección. La línea S' tangente a todos los frentes secundarios Sᵢ y que los envuelve resulta ser otra circunferencia y constituye el nuevo frente de ondas para ese instante posterior

t = t + Δt

Reflexión y refracción de las ondas

Cuando una onda alcanza la superficie de separación de dos medios de distinta naturaleza se producen, en general, dos nuevas ondas, una que retrocede hacia el medio de partida y otra que atraviesa la superficie límite y se propaga en el segundo medio. El primer fenómeno se denomina reflexión y el segundo recibe el nombre de refracción.

En las ondas monodimensionales como las producidas por la compresión de un muelle, la reflexión lleva consigo una inversión del sentido del movimiento ondulatorio. En las ondas bi o tridimensionales la inversión total se produce únicamente cuando la incidencia es normal, es decir, cuando la dirección, en la que avanza la perturbación es perpendicular a la superficie reflectante. Si la incidencia es oblicua se produce una especie de rebote, de modo que el movimiento ondulatorio reflejado cambia de dirección, pero conservando el valor del ángulo que forma con la superficie límite.

En el caso de las ondas sonoras, la reflexión en una pared explica el fenómeno del eco. Si la distancia a la pared es suficiente, es posible oír la propia voz reflejada porque el tiempo que emplea el sonido en ir y volver permite separar la percepción de la onda incidente de la reflejada. El oído humano sólo es capaz de percibir dos sonidos como separados si distan uno respecto del otro más de 0,1 segundos, de ahí que para que pueda percibiese el eco la superficie reflectiva debe estar separada del observador 17 metros por lo menos, cantidad que corresponde a la mitad de la distancia que recorre el sonido en el aire en ese intervalo de tiempo (17 m = 340 m/s·0,1 s/2).

En los espacios cerrados, como las salas, el sonido una vez generado se refleja sucesivas veces en las paredes, dando lugar a una prolongación por algunos instantes del sonido original. Este fenómeno se denomina reverberación y empeora las condiciones acústicas de una sala, puesto que hace que los sonidos anteriores se entremezclen con los posteriores. Su eliminación se logra recubriendo las paredes de materiales, como corcho o moqueta, que absorben las ondas sonoras e impiden la reflexión.

El fenómeno de la refracción supone un cambio en la velocidad de propagación de la onda, cambio asociado al paso de un medio a otro de diferente naturaleza o de diferentes propiedades. Este cambio de velocidad da lugar a un cambio en la dirección del movimiento ondulatorio. Como consecuencia, la onda refractada se desvía un cierto ángulo respecto de la incidente.

La refracción se presenta con cierta frecuencia debido a que los medios no son perfectamente homogéneos, sino que sus propiedades y, por lo tanto, la velocidad de propagación de las ondas en ellos, cambian de un punto a otro. La propagación del sonido en el aire sufre refracciones, dado que su temperatura no es uniforme. En un día soleado las capas de aire próximas a la superficie terrestre están más calientes que las altas y la velocidad del sonido, que aumenta con la temperatura, es mayor en las capas bajas que en las altas. Ello da lugar a que el sonido, como consecuencia de la refracción, se desvía hacia arriba. En esta situación la comunicación entre dos personas suficientemente separadas se vería dificultada. El fenómeno contrario ocurre durante las noches, ya que la Tierra se enfría más rápidamente que el aire.

Interferencias y pulsaciones

Cuando dos ondas de igual naturaleza se propagan simultáneamente por un mismo medio, cada punto del medio sufrirá la perturbación resultante de componer ambas. Este fenómeno de superposición de ondas recibe el nombre de interferencias y constituye uno de los más representativos del comportamiento ondulatorio.

Lo esencial del fenómeno de interferencias consiste en que la suma de las dos ondas supuestas de igual amplitud no da lugar necesariamente a una perturbación doble, sino que el resultado dependerá de lo retrasada o adelantada que esté una onda respecto de la otra. Se dice que dos ondas alcanzan un punto dado en fase cuando ambas producen en él oscilaciones sincrónicas o acompasadas. En tal caso la oscilación resultante tendrá una amplitud igual a la suma de las amplitudes de las ondas individuales, y la interferencia se denomina constructiva porque en la onda resultante se refuerzan los efectos individuales. Si por el contrario las oscilaciones producidas por cada onda en el punto considerado están contrapuestas, las ondas llegan en oposición de fase y la oscilación ocasionada por una onda será neutralizada por la debida a la otra. En esta situación la interferencia se denomina destructiva.

Si se consideran ondas armónicas unidimensionales y de igual frecuencia, el fenómeno de interferencias puede ser entendido como una consecuencia de las diferencias de distancia de los dos focos O₁ y O₂ al punto genérico P del medio considerado. Si en la diferencia entre O₁P y O₂P caben un número entero de ondas completas (y de longitudes de onda), eso significa que las ondas individuales llegan en fase a P. Si por el contrario caben un número impar de medias ondas (de semilongitudes de onda λ/2), equivale a decir que las ondas individuales llegan en oposición de fase.

De acuerdo con lo anterior, según sea la posición del punto P del medio respecto de los focos, así será el tipo de interferencias constructiva o destructivo que se darán en él. Cuando se estudia el medio en su conjunto se aprecian puntos en los que ha habido refuerzo y puntos en los que ha habido destrucción mutua de las perturbaciones. Cada uno de tales conjuntos de puntos forman líneas alternativas. El conjunto de líneas de máxima amplitud y de mínima amplitud de oscilación resultante constituye el esquema o patrón de interferencias.

Si se hace sonar un silbato en un recinto cuyas paredes reflejen bien el sonido, la superposición de las ondas incidente y reflejada daría lugar a un fenómeno de interferencias. Un observador que se desplazara por la sala, distinguiría unas posiciones en las cuales la intensidad del sonido percibido es máximo de otras en donde es prácticamente nulo. Para una frecuencia constante la intensidad del sonido fisiológico depende del cuadrado de la amplitud, pero no de la elongación, de modo que el oído no capta la vibración, sino que percibe una sensación regular que en los fenómenos de interferencia cambia de magnitud con la posición.

Cuando las ondas que se superponen tienen frecuencia ligeramente diferentes el fenómeno de interferencias sucede en el tiempo, es decir, sin desplazarse de un punto a otro un observador de ondas sonoras percibiría variaciones de intensidad pulsantes u oscilantes que reciben el nombre de pulsaciones. La suma geométrica de dos ondas sinusoidales de frecuencias o de períodos próximos demuestra que la onda resultante no tiene una amplitud constante, sino que varía a lo largo del tiempo. Se dice que es una onda de amplitud modulada. Si la amplitud varía, también variará la intensidad del sonido correspondiente, el cual es percibido fuerte y débil de un modo alternativo.

La difracción

Las ondas son capaces de traspasar orificios y bordear obstáculos interpuestos en su camino. Esta propiedad característica del comportamiento ondulatorio puede ser explicada como consecuencia del principio de Huygens y del fenómeno de interferencias.

Así, cuando una fuente de ondas alcanza una placa con un orificio o rendija central, cada punto de la porción del frente de ondas limitado por la rendija se convierte en foco emisor de ondas secundarias todas de idéntica frecuencia. Los focos secundarios que corresponden a los extremos de la abertura generan ondas que son las responsables de que el haz se abra tras la rendija y bordee sus esquinas. En los puntos intermedios se producen superposiciones de las ondas secundarias que dan lugar a zonas de intensidad máxima y de intensidad mínima típicas de los fenómenos de interferencias.

Ambos fenómenos que caracterizan la difracción de las ondas dependen de la relación existente entre el tamaño de la rendija o del obstáculo y la longitud de onda. Así, una rendija cuya anchura sea del orden de la longitud de la onda considerada, será completamente bordeada por la onda incidente y, además, el patrón de interferencias se reducirá a una zona de máxima amplitud idéntica a un foco. Es como si mediante este procedimiento se hubiera seleccionado uno de los focos secundarios descritos por Huygens en el principio que lleva su nombre.

El efecto Doppler

La frecuencia de un sonido está determinada por la frecuencia de la vibración que lo origina siempre que el foco que lo emite y el observador que lo percibe estén ambos en reposo. Cuando, ya sea el foco, ya sea el observador, están en movimiento, el sonido percibido presenta una frecuencia que depende de la velocidad. Un observador situado ante la vía del tren aprecia que el sonido emitido por el silbato de una locomotora que pasa delante de él a gran velocidad es más agudo cuando se acerca (mayor frecuencia, f) y más grave cuando se aleja (menor frecuencia). Este efecto, según el cual la frecuencia percibido de un sonido depende del estado de movimiento del observador, del foco o de ambos, fue explicado por primera vez en 1.842 por el físico austríaco Christian Doppler (1.803 - 1.853).

Si, como en el caso de la locomotora, el observador O está en reposo y el foco emisor F de ondas sonoras está en movimiento, sucede que debido al avance del foco los frentes de ondas se comprimen en el sentido del movimiento. Es como si cada frente de ondas tendiera a alcanzar al emitido en un instante anterior. Lo contrario sucede en el sentido opuesto al movimiento y los frentes de ondas se separan. El movimiento del foco da lugar, en definitiva, a frentes de ondas excéntricos.

El cambio en la distancia entre los frentes de ondas equivale a una modificación en la longitud de onda λ correspondiente y consiguientemente en la frecuencia observada. La nueva f' puede expresarse en términos matemáticos en la forma.

Donde v es la velocidad del sonido y v_F la velocidad del foco. El término v_F·T representa el espacio que recorre el foco en un intervalo de tiempo igual a un período T y, por tanto, la corrección que hay que aplicar a la longitud de onda λ (espacio recorrido por el sonido en un período T) medida en ausencia de movimiento. Dicha corrección es positiva cuando el foco se acerca al observador y negativa cuando se aleja de él.

Expresando la anterior ecuación de modo que figure en ella la frecuencia f = v/λ del sonido que se percibiría si el foco estuviera en reposo, se tiene:

f' = f/(1 ± v_F/v) (+) si F se aleja de O y (-) si F se acerca a O sin más que dividir numerador y denominador por λ.

Esta fórmula predice un salto de frecuencia de un tono musical completo si el foco pasa por delante del observador a 67 km/h. El propio Christian Doppler organizó experimentos con trompetas dispuestas en vagones para comprobar la validez de sus explicaciones teóricas. Músicos profesionales, expertos en la apreciación de los tonos, hicieron las veces de instrumentos de medida de los saltos de frecuencia en sus experiencias.

Si es el observador el que se desplaza a una velocidad v₀ estando el foco en reposo, los frentes de onda mantienen en este caso su carácter concéntrico, pero la frecuencia percibido, es decir, el número de ellos que llegan al observador en la unidad de tiempo, será diferente. Si el observador se acerca al foco las velocidades de ambos se sumarán y se restarán si se aleja de él. Por tanto:

Expresión que puede escribirse en la forma:

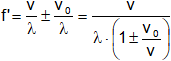
Es decir:

f' = f·(1 ± v₀/v) < 0 si "O" se aleja de F y, f' = f·(1 ± v₀/v) < 0 si "O" se acerca a F.

Siendo f' la frecuencia percibido por el observador y f la frecuencia emitida por el foco.

Ejemplo de la noción de interferencias

El resultado de la superposición de dos movimientos ondulatorios de igual frecuencia en un punto determinado del medio depende de la relación existente entre las diferencias de distancias entre los focos respectivos y el punto considerado. Llamando a dicha diferencia, las condiciones de máximo y de mínimo en el movimiento resultante se pueden escribir en la forma:

Máximo Δ = n·λ

n = 0, 1, 2, 3, … (en Δ cabe un número entero de ondas n completas)

Mínimo Δ = ½·(2·n + 1)·λ

n = 0, 1, 3, … (en Δ cabe un número impar de semiondas n)

Un experimentador conecta dos tubos de goma a la caja de un diapasón que es excitado eléctricamente y mantiene los otros extremos de los tubos en sus oídos. Aumentando progresivamente la longitud de uno de ellos, aprecia que cuando la diferencia entre ambos es de 18 cm percibe por primera vez un sonido de intensidad mínima. Se trata de determinar cuál es la frecuencia del diapasón y la longitud de la onda sonora correspondiente. (Considérese la velocidad del sonido en el aire 340 m/s)

En este caso el diapasón equivale a dos focos, al generar ondas idénticas que se propagan por caminos diferentes. Si el primer mínimo se consigue cuando es igual a 18 cm, aplicando la condición de mínimo se tendrá:

Δ = ½·(2·n + 1)·λ con n = 0

Luego:

λ = 2·Δ = 2·0,18 = 0,36 m

Dado que la frecuencia f y la longitud de onda λ están relacionadas por la ecuación

v = λ·f

Se tendrá:

Ejemplo del efecto Doppler

Una lancha rápida se acerca a la pared vertical de un acantilado en dirección perpendicular. Con la ayuda de un aparato de medida el piloto aprecia que entre el sonido emitido por la sirena de su embarcación y el percibido tras la reflexión en la pared del acantilado se produce un salto de frecuencias de 440 Hz a 495 Hz. ¿A qué velocidad navega la lancha? (Tómese la velocidad del sonido en el aire v = 340 m/s.)

El dato de la frecuencia inicial, 440 Hz, corresponde al valor en reposo, ya que el piloto, al moverse con la embarcación, está en reposo respecto de ella; por contra, el dato del sonido reflejado corresponde a una frecuencia emitida en movimiento. Se trata de averiguar, antes de pasar a las ecuaciones, si la situación es la de un foco en movimiento, la de un observador en movimiento o la de ambos en movimiento.

Si el observador estuviera situado en el acantilado se trataría, en efecto, del primer caso, pero por una parte la pared refleja la excentricidad de los frentes producida por el avance del foco -equivale a un foco en movimiento- y por otra, el observador se acerca a ese foco ficticio; luego la situación es la planteada en tercer lugar.

Las ecuaciones características del efecto Doppler indican lo siguiente:

Observador (O) en movimiento y foco (F) en reposo:

f' = f·(1 + v₀/v) si "O" se acerca a F.

Observador (O) en reposo y foco (F) en movimiento:

f' = f·(1 - v₀/v) si "O" se aleja de F.

Como se dan ambos casos, se aplicará sucesivamente ambas transformaciones a la frecuencia emitida f para obtener la frecuencia percibido f'

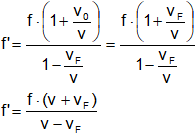
Pues en este caso v_F = v₀

Sustituyendo resulta:

Y despejando v_F se tiene:

v_F = 20 m/s = 72 km/h

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior
• |
• Siguiente ›