Ejemplo n° 5 de fuentes de energía

Ejemplo nº 5

Calcular la resistencia térmica total de un muro, formado por mampostería de 12 cm de espesor, una cámara de aire de 2 cm y un panderete de mampostería de 5 cm interior.

Desarrollo

Datos:

e₁ = 5 cm

e₂ = 12 cm

R_c = 2 cm

Fórmulas:

Esquema:

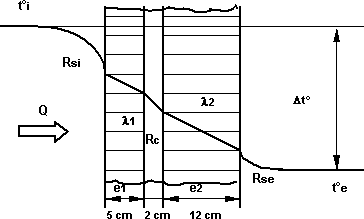
Esquema de la resistencia térmica total de un muro

Solución

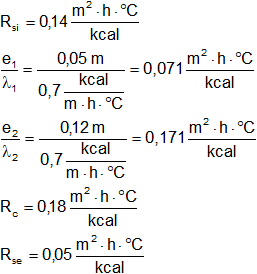
Rₜ = 0,61 m²·h·°C/kcal

O sea:

Reemplazamos por los valores y resolvemos:

k = 1,64 kcal/m²·h·°C

En este mismo ejemplo ¿qué pasaría si en lugar de la cámara de aire se utilizara lana de vidrio de 2 cm de espesor?

Rₜ = 0,489 m²·h·°C/kcal

Reemplazamos por los datos y resolvemos:

k = 1 kcal/m²·h·°C

Se aprecia, entonces, que mejora notablemente la resistencia térmica del muro aplicándole aislante térmico.

‹‹ Regresar al apunte: AP03

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la resistencia térmica de un muro