Ejemplo n° 11 de fuentes de energía
Ejemplo n° 11
Se tiene una resistencia eléctrica a la cual se le han medido las siguientes características:
U = 220 V
I = 1,75 A
cos φ = 0,95
Desarrollo
Datos:
U = 220 V
I = 1,75 A
cos φ = 0,95
V = 500 cm³
T = 120 s
Valor kW·h = $0,15
Fórmulas:
P = U·I·cos φ
| E = | P |
| t |
Q = m·cₑ·Δt
| H = | A·λ·Δt |
| e |
Solución
¿Qué Δt producirá esta resistencia eléctrica cuando calienta 500 cm³ de agua durante 120 segundos.
P = 220 v·1,75 A·0,95 ⇒ P = 365,75 W
| E = | P |
| t |
| E = | 365,75 W·120 s·1 h |
| 3.600 s |
E = 12,192 W·h
Sabiendo que 860 kcal = 1 kW
| E = 12,192 W·h· | 860 kcal | · | 1 kW |
| 1 kW | 1.000 W |
E = 10,485 kcal
| Δt = | Q |
| m·cₑ |
| Δt = | 10,485 kcal |
| 0,5 kg·1 kcal/kg·°C |
Δt = 20,97 °C
Hallar el costo:
Costo = Valor (kW·h)·E
Costo = (0,15 $/kW·h)·0,012192 kW·h
Costo = $ 0,0018
Hallar la temperatura final para (a) 45 min y (b) 20 min.
| H = | A·λ·Δt |
| e |
| H = | 0,055603 m²·0,03 cal/m²·h·°C·52 °C |
| 0,00952 m |
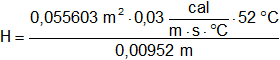
H = 7,97 kcal/h
a)
H₁ = 7,97 kcal/h·0,75 h
H₁ = 5,98 kcal
| Δt₁ = | H₁ |
| m·cₑ |
| Δt₁ = | 5,98 kcal |
| 0,5 kg·1 kcal/kg·°C |
Δt₁ = 11,96 °C
Resultado, la temperatura final para 45 min es:
t₁ = 60,04 °C
b)
H₂ = 7,97 kcal/h·0,33 h
H₂ = 2,63 kcal
| Δt₂ = | H₂ |
| m·cₑ |
| Δt₂ = | 2,63 kcal |
| 0,5 kg·1 kcal/kg·°C |
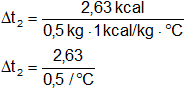
Δt₂ = 5,26 °C
Resultado, la temperatura final para 20 min es:
t₂ = 66,74 °C
Hallar la temperatura final para: c) 10 min; d) 30 min; e) 40 min; f) 50 min y g) 60 min, y luego graficar la temperatura en función del tiempo.
c)
H₃ = 7,97 kcal/h·0,17 h
H₃ = 1,35 kcal
| Δt₃ = | H₃ |
| m·cₑ |
| Δt₃ = | 1,35 kcal |
| 0,5 kg·1 kcal/kg·°C |
Δt₃ = 2,71 °C
Resultado, la temperatura final para 10 min es:
t₃ = 67,29 °C
d)
H₄ = 7,97 kcal/h·0,50 h
H₄ = 3,99 kcal
| Δt₄ = | H₄ |
| m·cₑ |
| Δt₄ = | 3,99 kcal |
| 0,5 kg·1 kcal/kg·°C |
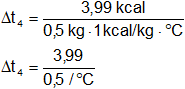
Δt₄ = 7,98 °C
Resultado, la temperatura final para 30 min es:
t₄ = 62,02 °C
e)
H₅ = 7,97 kcal/h·0,66 h
H₅ = 5,31 kcal
| Δt₅ = | H₅ |
| m·cₑ |
| Δt₅ = | 5,31 kcal |
| 0,5 kg·1 kcal/kg·°C |
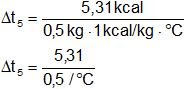
Δt₅ = 10,62 °C
Resultado, la temperatura final para 40 min es:
t₅ = 59,38 °C
f)
H₆ = 7,97 kcal/h·0,83 h
H₆ = 6,64 kcal
| Δt₆ = | H₆ |
| m·cₑ |
| Δt₆ = | 6,64 kcal |
| 0,5 kg·1 kcal/kg·°C |
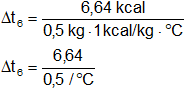
Δt₆ = 13,28 °C
Resultado, la temperatura final para 50 min es:
t₆ = 56,72 °C
g)
H₇ = 7,97 kcal/h·1 h
H₇ = 7,97 kcal
| Δt₇ = | H₇ |
| m·cₑ |
| Δt₇ = | 7,97 kcal |
| 0,5 kg·1 kcal/kg·°C |
Δt₇ = 15,94 °C
Resultado, la temperatura final para 60 min es:
t₇ = 54,06 °C
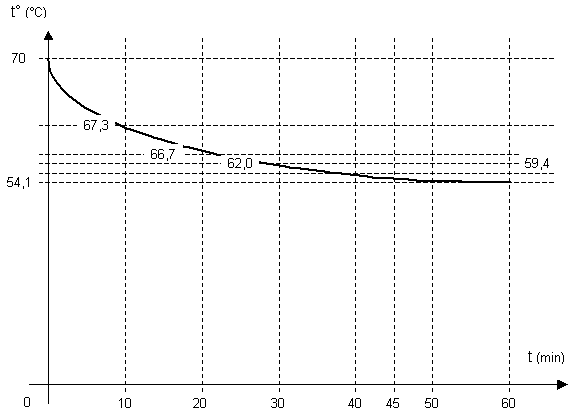
Gráfico de la temperatura en función del tiempo
Autor: Ricardo Santiago Netto. Argentina
Ejemplo, cómo calcular la cantidad de calor y el costo de una resistencia