Problema nº 9 de atraso del reloj de péndulo por la variación de la temperatura - TP01
Enunciado del ejercicio nº 9
¿Cuánto atrasa por día un reloj de péndulo de cobre, no compensado, que marcha exactamente a 0 °C, si se lo mantiene a 20 °C?
Desarrollo
Datos:
t₀ = 0 °C
t₂₀ = 20 °C
α = 0,0000165/°C
Fórmulas:
Δl = α·l₁·Δt°
| l = | T²·g |
| 4·π² |
Solución
De la fórmula de dilatación lineal despejamos l₂₀:
l₂₀ - l₀ = α·l₀·Δt°
l₂₀ = α·l₀·Δt° + l₀
l₂₀ = (α·Δt° + 1)·l₀ (1)
Planteamos las ecuaciones de la longitud del péndulo para cada temperatura:
| l₀ = | T₀²·g | (2) |
| 4·π² |
| l₂₀ = | T₂₀²·g |
| 4·π² |
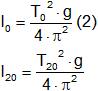
Reemplazamos l₂₀ por l₀:
| (α·Δt° + 1)·l₀ = | T₂₀²·g |
| 4·π² |
| l₀ = | T₂₀²·g | (3) |
| (α·Δt° + 1)·4·π² |
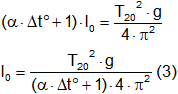
Igualamos las ecuaciones (2) y (3):
| T₀²·g | = | T₂₀²·g |
| 4·π² | (α·Δt° + 1)·4·π² |
Simplificamos:
| T₀² | = | T₂₀² |
| 1 | (α·Δt° + 1) |
T₂₀² = (α·Δt° + 1)·T₀²
Aplicamos raíz cuadrada en ambos términos:
√T₂₀² = √(α·Δt° + 1)·T₀²
T₂₀ = √α·Δt° + 1·T₀
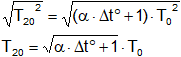
Reemplazamos por los valores y calculamos:
T₂₀ = √0,0000165/°C·(20 °C - 0 °C) + 1·T₀
T₂₀ = √0,0000165/°C·20 °C + 1·T₀
T₂₀ = √0,00033 + 1·T₀
T₂₀ = √1,00033·T₀
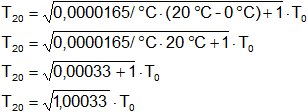
Obtenemos la relación de tiempo.
T₂₀ = 1,000164986·T₀
El enunciado pide la diferencia por día:
1 día = 24 h = 24·60·60 s
1 día = 86.400 s
| 1 s | ⟶ | 1,000164986 s |
| 86.400 s | ⟶ | t |
| t = | 86.400 s·1,000164986 s |
| 1 s |
t = 86.414,25482 s
Obtenemos la relación por día en segundos. Luego calculamos el tiempo en segundos:
Δt = 86.414,25482 s - 86.400 s
Δt = 14,25482407 s
Respuesta, el atraso del reloj de péndulo por día es:
Δt = 14,25 s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, ¿cuánto atrasa por día un reloj de péndulo?