Problema nº 10 de trabajo y potencia, variación de la energía mecánica - TP06

Enunciado del ejercicio nº 10

Por un plano inclinado de base 80 m y altura 10 m desciende un cuerpo de 600 kgf sin que se modifique su velocidad. Calcular la variación de la energía mecánica.

Desarrollo

Datos:

P = 600 kgf

h₁ = 0 m

h₂ = 10 m

b = 80 m

Fórmulas:

P = m·g

ΔE_M = ΔE_c + ΔEₚ

Eₚ = m·g·h

Esquema:

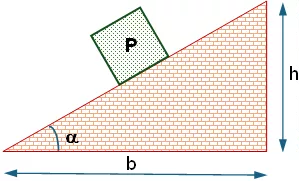
Esquema del plano inclinado y la fuerza

Solución

Aplicamos el teorema de la energía mecánica:

ΔE_M = ΔE_c + ΔEₚ

Si la velocidad permanece constante, entonces, la variación de la energía cinética es nula:

ΔE_M = ΔEₚ

ΔE_M = Eₚ₂ - Eₚ₁

ΔE_M = m·g·h₂ - m·g·h₁

Al final del plano inclinado la altura es nula:

h₂ = 0

ΔE_M = -m·g·h₁

Dado que:

P = m·g

Reemplazamos en la ecuación anterior:

ΔE_M = -P·h₁

Reemplazamos por los valores y calculamos:

ΔE_M = -600 kgf·10 m

ΔE_M = -6.000 kgf·m

Resultado, la variación de la energía mecánica es:

ΔE_M = -6.000 kgf·m

Es negativa porque al descender pierde energía potencial.

La longitud de la base no es dato.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la variación de la energía mecánica