Problema nº 2 de interpretación gráfica de posición en función del tiempo en el movimiento uniformemente variado (MUV) - TP07
Enunciado del ejercicio nº 2
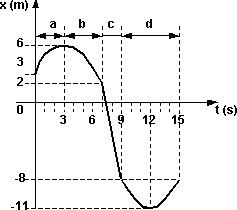
En la figura se indica la posición de un móvil en función del tiempo, hallar la velocidad media durante los intervalos de tiempo a, b, c y d indicados.
Solución
Para calcular la velocidad media aplicamos:
a)
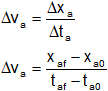
Reemplazamos por los valores y calculamos:
![]()
Resultado, la velocidad media en el intervalo a es:
Δvₐ = 1 m/s
b)
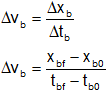
Reemplazamos por los valores y calculamos:
![]()
Resultado, la velocidad media en el intervalo b es:
Δvb = -1 m/s
c)
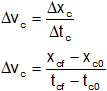
Reemplazamos por los valores y calculamos:
![]()
Resultado, la velocidad media en el intervalo c es:
Δvc = -5 m/s
d)
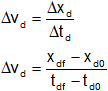
Reemplazamos por los valores y calculamos:
![]()
Resultado, la velocidad media en el intervalo d es:
Δvd = 0 m/s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP07
- | Siguiente ›
Ejemplo, cómo interpretar gráficas de posición en función del tiempo en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.