Problema nº 3 de interpretación gráfica de posición en función del tiempo en el movimiento uniformemente variado (MUV) - TP07

Enunciado del ejercicio nº 3

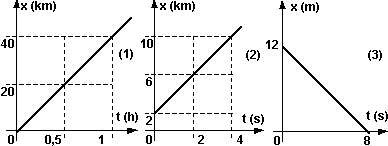
Hallar las pendientes de las tres rectas, expresándolas en las unidades correspondientes, luego analice si es correcto graficar a la izquierda del eje verical.

Solución

Δv₁ = Δx₁/Δt₁

Δv₁ = (x_1f - x₁₀)/(t_1f - t₁₀)

Δv₁ = (40 km - 0 km)/(1 h - 0 h)

Resultado, la pendiente del gráfico (1) indica una velocidad de:

Δv₁ = 40 km/h

Δv₂ = Δx₂/Δt₂

Δv₂ = (x_2f - x₂₀)/(t_2f - t₂₀)

Δv₂ = (10 km - 2 km)/(4 s - 0 s)

Resultado, la pendiente del gráfico (2) indica una velocidad de:

Δv₂ = 2 km/s

Δv₃ = Δx₃/Δt₃

Δv₃ = (x_3f - x₃ᵢ)/(t_3f - t₃ᵢ)

Δv₃ = (0 m - 12 m)/(8 s - 0 s)

Resultado, la pendiente del gráfico (3) indica una velocidad de:

Δv₃ = -1,5 m/s

No se puede graficar a la izquierda del eje vertical, no existe el tiempo negativo.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP07
• | Siguiente ›

Ejemplo, cómo interpretar gráficas de posición en función del tiempo en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.