Problema nº 1 de tiro o lanzamiento oblicuo, tiempo y posición - TP09

Enunciado del ejercicio nº 1

Un piloto, volando horizontalmente a 500 m de altura y 1.080 km/h, lanza una bomba. Calcular:

a) ¿Cuánto tarda en oír la explosión?

b) ¿A qué distancia se encontraba el objetivo?

Se recuerda que en tiro parabólico y tiro oblicuo el movimiento en el eje X es rectilíneo uniforme, mientras en el eje Y es uniformemente variado (asociar con tiro vertical y caída libre).

Donde no se indica se emplea g = 10 m/s²

Desarrollo

Datos:

vₓ = 1.080 km/h = 300 m/s

g = 10 m/s²

v_0y = 0 m/s

h = 500 m

Fórmulas:

v_fy = v_0y + g·t (1)

h = v_0y·t + ½·g·t² (2)

(3)

El gráfico es:

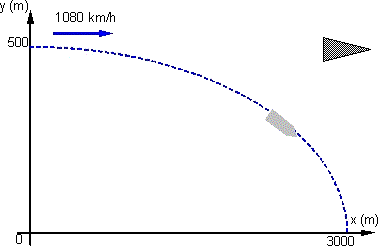
Solución

El tiempo que tarda en caer la bomba lo calculamos de la ecuación (2):

500 m = ½·(10 m/s²)·t²

500 m = (5 m/s²)·t²

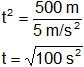
t = 10 s

La distancia recorrida por la bomba a lo largo del eje X será:

x = vₓ·t

x = (300 m/s)·(10 s)

Resultado, la distancia al objetivo es:

x = 3.000 m

En el mismo instante que la bomba toca el suelo el avión pasa sobre ella, es decir 500 m sobre la explosión.

Si la velocidad del sonido es 330 m/s:

Reemplazamos por los valores y calculamos:

t = 1,52 s

a)

t = 10 s + 1,52 s

Resultado, el tiempo que demora en oír la explosión es:

t = 11,52 s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP09
• | Siguiente ›

Ejemplo, cómo calcular el tiempo y la posición en el movimiento uniforme variado. Lanzamiento oblicuo. Nivel medio, secundaria, bachillerato, ESO.