Problema nº 2 de tiro o lanzamiento oblicuo, tiempo y posición - TP09

Enunciado del ejercicio nº 2

Un avión que vuela a 2.000 m de altura con una velocidad de 800 km/h suelta una bomba cuando se encuentra a 5.000 m del objetivo. Determinar:

a) ¿A qué distancia del objetivo cae la bomba?

b) ¿Cuánto tarda la bomba en llegar al suelo?

c) ¿Dónde esta el avión al explotar la bomba?

Se recuerda que en tiro parabólico y tiro oblicuo el movimiento en el eje X es rectilíneo uniforme, mientras en el eje Y es uniformemente variado (asociar con tiro vertical y caída libre).

Donde no se indica se emplea g = 10 m/s²

Desarrollo

Datos:

vₓ = 800 km/h = 222,22 m/s

v_0y = 0 m/s

h = 2.000 m

d = 5.000 m

Fórmulas:

v_fy = v_0y + g·t (1)

h = v_0y·t + ½·g·t² (2)

vₓ =	Δx	(3)
	Δt

El gráfico es:

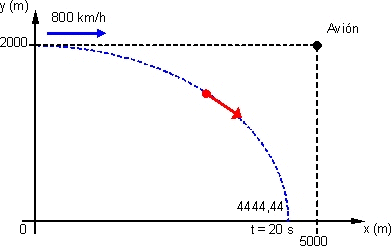
Gráfica de la trayectoria de tiro oblicuo

Solución

Primero calculamos el tiempo que demora en caer, de la ecuación (2):

h = ½·g·t²

t = √2·h/g

t = √2·2.000 m/(10 m/s²)

t = 20 s

Luego con la ecuación (3) obtenemos el punto de impacto:

vₓ =	x
	t

x = vₓ·t

x = (222,22 m/s)·(20 s)

x = 4.444,44 m

Por lo tanto el proyectil cae a:

d = 5.000 m - 4.444,44 m

Resultado, la distancia entre el objetivo y la bomba es:

d = 555,55 m

Es el tiempo hallado anteriormente:

Resultado, el tiempo que tarda la bomba en llegar al suelo es:

t = 20 s

Resultado, sobre la bomba, ambos mantienen la misma velocidad en el eje X.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular el tiempo y la posición en el movimiento uniforme variado. Lanzamiento oblicuo. Nivel medio, secundaria, bachillerato, ESO.