Ejemplo, cómo calcular el tiempo, la velocidad final y la altura en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.

Problema n° 1 de tiro vertical - TP13

Enunciado del ejercicio n° 1

Se lanza una pelota desde lo alto de un faro de 80 m de altura, con una velocidad inicial de 4 m/s hacia abajo.

a) ¿Cuánto tarda en llegar al suelo?

b) ¿Con qué velocidad llega?

c) ¿A qué altura está luego de 2 s de haberla arrojado?

Usar g = 10 m/s²

v₀ = 4 m/s

h = 80 m

(1) v_f = v₀ + g·t

(2) y = v₀·t + ½·g·t²

(3) v_f² - v₀² = 2·g·h

De la ecuación (2):

0 = v₀·t + ½·g·t² - y

Aplicamos la ecuación cuadrática (Báscara o Bhaskara) que dará dos resultados:

t_1,2 =	-v₀ ± √v₀² - 4·½·g·(-y)
	2·½·g

t_1,2 =	-v₀ ± √v₀² + 2·g·y
	g

t_1,2 =	-(-4 m/s) ± √(-4 m/s)² + 2·(-10 m/s²)·(-80 m)
	-10 m/s²

t_1,2 =	4 m/s ± √16 m²/s² + 1.600 m²/s²
	-10 m/s²

t_1,2 =	4 m/s ± √1.616 m²/s²
	-10 m/s²

t_1,2 =	4 m/s ± 40,2 m/s
	-10 m/s²

t₁ =	4 m/s + 40,2 m/s
	-10 m/s²

t₂ =	4 m/s - 40,2 m/s
	-10 m/s²

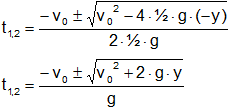
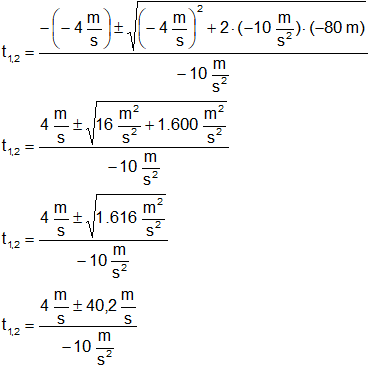
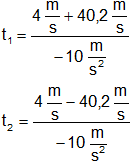
Resultado, el tiempo que tarda en llegar al suelo es:

t₁ = -4,42 s (No es solución)

t₂ = 3,62 s

De la ecuación (1):

v_f = 4 m/s + (10 m/s²)·(3,62 s)

Resultado, la velocidad con que llegar al suelo es:

v_f = 40,20 m/s

Empleando la ecuación (2):

y = (4 m/s)·(2 s) + ½·(10 m/s²)·(2 s)²

y = 28 m (descendió)

La altura es:

h = 80 m - 28 m

Resultado, la altura a los 2 s del lanzamiento es:

h = 52 m

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.