Problema nº 7 de tiro parabólico, altura máxima - TP22

Enunciado del ejercicio nº 7

Se dispara un proyectil con un cañón que forma un ángulo de 60° con respecto a la horizontal, si la velocidad del proyectil al momento de dejar la boca del cañón es de 400 m/s.

¿Cuál es la altura máxima que alcanza el proyectil? (g = 10 m/s²)

Desarrollo

Datos:

α = 60°

v = 400 m/s

g = 10 m/s²

Fórmulas:

v_f² = v₀² + 2·g·Δy

El gráfico es:

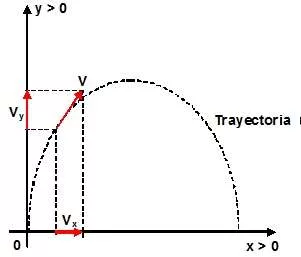
Gráfica del tiro parabólico

Solución

Primero calculamos la componente vertical de la velocidad (v_y):

v_y = v·(sen α)

v_y = (400 m/s)·sen 60°

v_y = (400 m/s)·0,866

v_y = 346,41 m/s

En el tiro parabólico, el movimiento sobre el eje Y es igual que en el "Tiro vertical", y valen todas sus ecuaciones.

Para calcular la altura máxima, debemos considerar que ocurre cuando la velocidad en Y se hace "cero", es decir que la velocidad final será cero:

v_f = 0 m/s

La velocidad inicial es la calculada anteriormente (v_y = 346,41 m/s).

Podemos aplicar la fórmula (para el eje Y):

v_f² = v₀² + 2·g·Δy

0² = v₀² + 2·g·Δy

-v₀² = 2·g·Δy

Resultado, la altura máxima que alcanza el proyectil es:

Δy = 6.000 m

Problema corregido por: Daniel Maeda.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP22
• | Siguiente ›

Ejemplo, cómo calcular la altura máxima en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.