Problema nº 10 de dinámica, tensiones de cuerdas en un movimiento por etapas - TP01

Enunciado del ejercicio nº 10

Un paracaidista de 80 kgf de peso, salta a 5.000 m de altura. Abre su paracaídas a 4.820 m y en 10 s reduce su velocidad a la mitad. Calcular la tensión en cada uno de los 12 cordones que tiene el paracaídas.

Desarrollo

Datos:

P = 80 kgf

h₁ = 5.000 m

h₂ = 4.820 m

t₃ = 10 s

g = 9,81 m/s²

Cordones = 12

Fórmulas:

v_f² - vᵢ² = 2·g·Δh (1)

v_f - vᵢ = a·t (2)

F = m·a (3)

P = m·g (4)

Solución

Los primeros metros del paracaidista son en caída libre con el paracaídas cerrado:

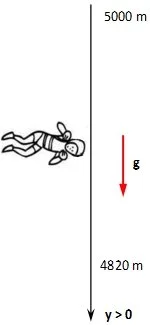
Esquema del movimiento con paracaídas cerrado, caída libre

Luego abre el paracaídas:

Esquema del movimiento con paracaídas abierto, caída frenada

Hasta aquí diferenciamos las etapas del movimiento.

Primero convertimos los 80 kgf a newton (N):

P = 80 kgf·(9,80665 N)/(1 kgf) = 784,532 N

P = 784,532 N

Y calculamos la masa que la usaremos más adelante:

P = m·g

Reemplazamos por los valores y calculamos:

m = 80 kg (5)

Luego, tenemos un movimiento de caída libre desde los 5.000 m a los 4.820 m, aplicamos la ecuación (1) para determinar la velocidad final de la caída que, a su vez, será la velocidad inicial del frenado ocasionado por la apertura del paracaídas:

v₂² - v₁² = 2·g·Δh

La velocidad inicial es nula (v₁ = 0 m/s):

v₂² = 2·g·Δh

Reemplazando por los datos:

v₂² = 2·(9,81 m/s²)·(5.000 m - 4.820 m)

v₂² = 2·(9,81 m/s²)·180 m

v₂² = 3.530,394 m²/s²

v₂ = 59,42 m/s

En éste momento se abre el paracaídas, a partir de aquí la velocidad se reduce a la mitad en los próximos 10 segundos:

v₃ = ½·v₂

v₃ = ½·(59,42 m/s)

v₃ = 29,71 m/s

Para lograr ésta disminución de la velocidad el paracaídas ejerció una fuerza de frenado cuya desaceleración la calculamos con la ecuación (2):

v₃ - v₂ = a·t

Despejamos a:

Reemplazamos por los valores:

Cálculo de la aceleración

a = -2,971 m/s²

Esta es la aceleración de la fuerza de frenado o desaceleración ocasionada por la apertura del paracaídas.

Ahora calculamos la fuerza que ejerce todo el paracaídas con la ecuación (3) y la masa (5):

F = m·a

F = 80 kg·(-2,971 m/s²)

F = -237,67 N

Sólo falta repartir ésta fuerza entre la tensión T de cada uno de los 12 cordones:

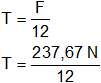
Cálculo de la tensión

Resultado, la tensión en cada uno de los cordones del paracaídas es:

T = 19,81 N

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular tensiones de cuerdas en un movimiento por etapas.