Problema nº 7 de dinámica, fuerza de reacción - TP05
Enunciado del ejercicio nº 7
La masa de un elevador es de 200 kg y la de una persona que está dentro de él es de 80 kg.
Si la tensión en el cable que sube al elevador es de 300 kgf, ¿cuál es la fuerza que ejerce el piso del elevador sobre la persona?
Desarrollo
Datos:
T = 300 kgf
mA = 200 kg
mP = 80 kg
g = 9,80665 m/s²
Fórmulas:
F = m·a
P = m·g
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
Esquema:
Diagrama del cuerpo libre
Solución
Convertimos las unidades:
| T = 300 kgf· | 9,80665 N | = 2.941,995 N |
| 1 kgf |
La condición de equilibrio es:
∑F = 0
Pero como hay movimiento:
∑F = m·a
Las fuerzas sobre el eje (tomando el eje positivo hacia arriba) son:
T - PA - PP = mₜ·a
P = m·g
Reemplazamos:
T - mA·g - mP·g = mₜ·a
Hallamos la aceleración del sistema. Despejamos a:
| a = | T - mA·g - mP·g |
| mₜ |
| a = | T - mA·g - mP·g |
| mA + mP |
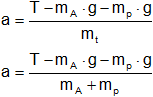
Reemplazamos con los datos y calculamos:
| a = | 2.941,995 N - 200 kg·9,80665 m/s² - 80 kg·9,80665 m/s² |
| 200 kg + 80 kg |
| a = | 2.941,995 N - 1.961,33 N - 784,532 N |
| 280 kg |
| a = | 196,133 N |
| 280 kg |
a = 0,700475 m/s²
Con este dato planteamos la ecuación de la fuerza sobre la persona:
F = PP + mA·a
F = mA·g + mA·a
Reemplazamos con los datos y calculamos:
F = 80 kg·9,80665 m/s² + 80 kg·0,700475 m/s²
F = 784,532 N + 56,038 N
F = 840,57 N
Resultado, la fuerza que ejerce el piso del elevador sobre la persona es:
F = 840,6 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo de cuerpos suspendidos, como calcular la fuerza de reacción