Campo eléctrico - Intensidad de campo
Intensidad de campo
Un cuerpo o una partícula cargada eléctricamente crea a su alrededor una propiedad denominada campo eléctrico que hace que al colocar cualquier otro cuerpo dotado de carga eléctrica en sus proximidades actúe sobre él una fuerza eléctrica.
Si sobre q aparece una fuerza diremos que estamos dentro del campo eléctrico de Q.
F = 0
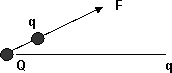
Esquema del campo eléctrico
![]()
Si d = ∞ ⟶ F = 0
El campo eléctrico llega al ∞. (el ∞ depende de la cantidad de carga, 2 e⁻ a 15 metros es como si estuvieran en el infinito).
Se define intensidad del campo eléctrico Ē en un punto como la fuerza a la que estaría sometida la unidad de carga positiva colocada en dicho punto.
![]() ⟶ N/C
⟶ N/C
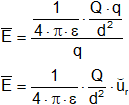
Está definida en cualquier punto del campo. El sentido del campo coincide con el sentido del movimiento que adquiriría una carga positiva colocada en dicho punto
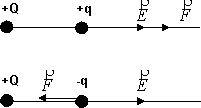
Sentido del campo eléctrico
Campo en el interior de un conductor en equilibrio
Las cargas de un conductor tienen libertad de movimiento. Si situamos un conductor en un campo eléctrico las cargas se ven sometidas a fuerzas eléctricas que las empujan a la superficie del conductor.
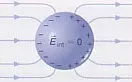
El conductor alcanza el equilibrio cuando sus cargas libres estén en reposo. En esta situación, las cargas eléctricas están totalmente distribuidas en la superficie del conductor de modo que el campo eléctrico en el interior del conductor es nulo.
Líneas de fuerza. Campo uniforme
Los campos vectoriales se representan por líneas vectoriales. Como el campo es una fuerza son líneas de fuerza.
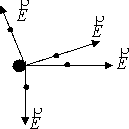
Esquema de las líneas de fuerza en un campo uniforme
Líneas de fuerzas del campo eléctrico son líneas imaginarias y son la trayectoria que seguiría la unidad de carga positiva dejada en libertad dentro del campo eléctrico.
Criterios para dibujarlas
1) Las líneas de fuerza salen de las cargas positivas (fuentes) y entran en las cargas negativas (sumideros). Si no existen cargas positivas o negativas las líneas de campo empiezan o terminan en el infinito
2) El número de líneas que entran o salen de una carga puntual es proporcional al valor de la carga
3) En cada punto del campo, el número de líneas por unidad de superficie perpendicular a ellas es proporcional a la intensidad de campo
4) Dos líneas de fuerza nunca pueden cortarse. (El campo en cada punto tiene una dirección y un sentido único. En un punto no puede haber dos líneas de fuerza ya que implicaría dos direcciones para el campo eléctrico

Una carga puntual positiva | 
Una carga puntual negativa |

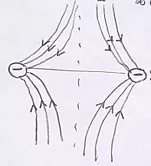
Dos cargas puntuales del mismo signo | 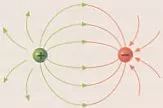
Dos cargas puntuales de diferente signo |
Podemos definir la intensidad de campo utilizado el concepto de líneas de fuerza.
Líneas de fuerza en un campo eléctrico
Es el número de líneas de fuerza que atraviesan la unidad de superficie colocada perpendicularmente a dichas líneas.

Intensidad de campo y líneas de fuerza
Campo uniforme:
|
a) Suponemos líneas paralelas b) EA = EB |
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué son las líneas de fuerza del campo eléctrico? ¿Qué es el campo eléctrico? Ejemplos. ¿Qué es el flujo del campo eléctrico? ¿Qué dice la ley de Gauss?
