Estática: Vectores y representación de fuerzas en física
Fuerza, gravedad y peso
De nuestra experiencia sensorial tenemos una noción intuitiva de fuerza. Sabemos que para sostener un cuerpo debemos efectuar un esfuerzo muscular que llamamos fuerza y admitimos que esa fuerza tiene por objeto equilibrar la que ejerce el cuerpo como consecuencia de la atracción terrestre. Esta atracción se llama fuerza de gravedad o peso.

La pesa se sostiene por el esfuerzo muscular | 
La plomada indica la dirección de la vertical |
Si el cuerpo está colgado de un hilo, ésta toma una posición que llamamos vertical y nos determina la dirección de la fuerza de gravedad, que prácticamente coincide con la del radio terrestre.
El sentido de la fuerza es de arriba hacia abajo.
Por analogía, cuando observamos un cuerpo colgado o apoyado sobre otro decimos que ejerce una fuerza sobre él.
También cunado queremos desplazar un cuerpo aplicamos sobre él nuestro esfuerzo muscular (una fuerza), y cuando observamos que un cuerpo comienza a moverse por acción de otro decimos que el segundo ha ejercido una fuerza sobre el primero.
Esta acción (fuerza) puede no ser transmitida por contacto directo; así, un imán ejerce una fuerza de atracción sobre un trozo de hierro separado de él, ya la atracción de la Tierra (peso) se manifiesta sin que los cuerpos estén en contacto con ella.
El concepto de fuerza, que no estamos definiendo, aparece asó como una extensión al mundo físico, de una noción puramente subjetiva.

Vectores: Son modelos matemáticos.
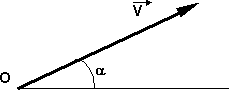
Sea el vector V, representa una cantidad física, se compone de:
1) Módulo: (magnitud) valor numérico y absoluto del mismo, expresa la cantidad que representa el mismo y se le asigna una unidad
2) Dirección: recta de acción, que según el sistema de referencia posee una inclinación α
3) Sentido: según el sistema de referencia, tendrá signo positivo o negativo
4) Origen: punto de aplicación
Fuerza
Magnitud física que se representa con un vector y su unidad puede ser newton (N), kilogramo fuerza (kgf) o dina.
Resultante
La fuerza resultante es la suma vectorial de todas las fuerzas aplicadas y no aplicadas a un sistema.
Momento o torque de una fuerza
El momento de una fuerza es el producto vectorial de dicha fuerza por la distancia perpendicular a un determinado eje de giro. Cuando se aplica una fuerza a una puerta pesada para abrirla, la fuerza se ejerce perpendicularmente a la puerta y a la máxima distancia de las bisagras. Así se logra un momento máximo. Si se empujara la puerta con la misma fuerza en un punto situado a medio camino entre el tirador y las bisagras, la magnitud del momento sería la mitad. Si la fuerza se aplicara de forma paralela a la puerta (es decir, de canto), el momento sería nulo.
M = F×d·sen α
Si α = 90°:
M = F×d (torque máximo)
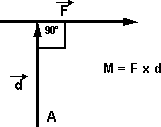
Sea el vector distancia, un vector perpendicular a una fuerza, de magnitud igual a la distancia entre un punto a y la recta de acción de la fuerza, se define como vector momento de la fuerza con respecto al punto a:
| Sentido horario - F 
| Sentido antihorario + F 
|
El producto vectorial entre el vector fuerza y el vector distancia, cuya dirección es perpendicular al plano que forman el punto A y la fuerza y, el sentido dependerá del vector fuerza (horario - antihorario).
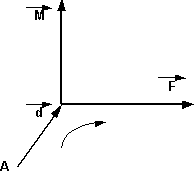
Vista tridimensional según la regla del tirabuzón (para la mano izquierda)
Las unidades del vector momento son: N·m, kilográmetro (kgm) ó dina·cm por ser éste un producto vectorial.
Autor: Ricardo Santiago Netto. Argentina
¿Cuál es el objeto de estudio de la estática?