Problema nº 4 de gases ideales, presión de un gas con el cambio de volumen - TP02

Enunciado del ejercicio nº 4

Un tubo cilíndrico de 1,5 m de largo se sumerge verticalmente en mercurio hasta que el extremo cerrado queda a 25 cm de la superficie libre del mercurio. Determinar la longitud que ocupará, dentro del tubo, el aire, si la presión exterior es de 75 cm de Hg (δ = 13,56 g/cm³).

Desarrollo

Datos:

l = 1,5 m

Δl = 25 cm = 0,25 m

p = 75 cm Hg

δ = 13,56 g/cm³

Convertimos las unidades de presión:

p = 99.991,7763 Pa

Convertimos las unidades de densidad:

δ = 13.560 kg/m³

Fórmulas:

Esquema:

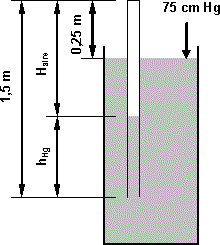
Esquema del barómetro

Esquema del barómetro

Solución

Aplicamos la ecuación general de los gases ideales. Para el caso:

p₁·V₁ = p₂·V₂

Pero el volumen es:

p₁·π·r²·h₁ = p₂·π·r²·h₂

Como la sección es uniforme:

p₁·h₁ = p₂·h₂

(1)

Siendo:

h₁: 1,50 m

h₂: la altura buscada.

p₁: es la presión inicial, la atmosférica.

p₂: es la presión final, presión que el aire ejerce sobre el mercurio.

Según el esquema y el enunciado la presión en la boca del tubo es:

p = p₀ + δ·g·h

Donde:

p₀: es la presión atmosférica (p₁).

h: es la altura del mercurio (1,25 m).

Siendo g = 9,80665 m/s²

p = 99.991,7763 Pa + (13.560 kg/m³)·(9,80665 m/s²)·1,25 m

p = 266.214,494 Pa

Esta presión se encuentra equilibrada con la interna del tubo, que esta ejercida por el aire. Aplicando la ecuación (1):

Reemplazamos por los valores y calculamos:

Resultado, la longitud que ocupará el aire es:

h₂ = 0,5634 m

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la presión de un gas con el cambio de volumen