Teorema de Ampere
El Teorema de Gauss relaciona el campo eléctrico con las cargas eléctricas y permite determinar el campo eléctrico para distribuciones de carga con simetría sencilla. Ahora vamos a obtener un Teorema que relaciona el campo magnético con sus fuentes, las corrientes eléctricas. El Teorema de Ampere nos permite determinar el campo magnético de algunas corrientes de simetría sencilla.
Se llama circulación del campo magnético a la integral, a lo largo de una trayectoria del producto escalar de B por dl.
∫C B·dl
Veamos la circulación del campo creado por una corriente I en una circunferencia de radio R centrada en un hilo conductor.
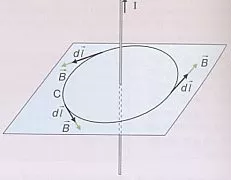
Diagrama de la circulación del campo magnético
B y dl son paralelos
| B = | μ₀·I |
| 2·π·R |
| ∮C | μ₀·I | · dl = | μ₀·I | ∮C dl = | μ₀·I | ·2·π·R = μ₀·I |
| 2·π·R | 2·π·R | 2·π·R |
El Teorema de Ampere es la generalización de este resultado:
"La circulación del campo magnético sobre cualquier curva cerrada C es igual al producto de la permeabilidad μ₀ por la intensidad de corriente que atraviesa la superficie limitada por la curva C".
∮C B·dl = μ₀·I
Consecuencia de esto es que la circulación de B en una superficie cerrada es # 0. Si calculamos la circulación de E a lo largo de una superficie cerrada será 0 por ser E conservativo. Por tanto B no es conservativo porque el campo depende de la v. (ver libro de Bruño si hay dudas)
Campo magnético en el interior de un solenoide
Supongamos un solenoide de N espiras, intensidad I y longitud l suficientemente largo.
En el interior del solenoide las líneas son paralelas y el campo constante.
En el exterior se puede considerar nulo.
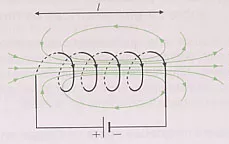
Representación del campo magnético en el interior de un solenoide
Para aplicar el Teorema de Ampere cogemos un rectángulo.
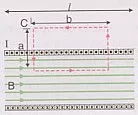
Diagrama para aplicar el teorema de Ampere en un solenoide
| ∮ B·dl = ∫ | a | B·dl + ∫ | c | B·dl + ∫ | d | B·dl + ∫ | a | B·dl |
| b | b | c | d |
La 2ª y 4ª son 0 porque B ⊥ dl. La 3ª es 0 porque B = 0 en el exterior. Si I es la intensidad que atraviesa una espira el solenoide será NI.
| ∮ B·dl = ∫ | a | B·dl = B·l = μ₀·N·I |
| b |
Por tanto;
| B = | μ₀·N·I |
| l |
Un toroide es como un solenoide de longitud 2·π·R
Ejemplo de un toroide
| B = | μ₀·N·I |
| 2·π·R |
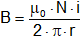
Campo electrostático | Campo magnético |
| Está originado por cargas eléctricas | Está originado por cargas eléctricas en movimiento |
| Las líneas de campo son líneas de fuerza abiertas. Su dirección es radial | Las líneas de campo no son líneas de fuerza, porque las fuerzas que origina el campo sobre las cargas eléctricas en movimiento, son perpendiculares al vector campo. Son siempre cerradas |
| Pueden existir cargas eléctricas separadas | No existen polos magnéticos aislados |
| Es conservativo, por lo que se puede definir una función potencial | No es conservativo, por lo que no tiene sentido definir una función potencial |
| La intensidad de la interacción depende del medio, siendo mayor en el vacío que en los medios materiales | La intensidad de la interacción depende del medio, pero, según el tipo del material, puede ser mayor o menor que en el vacío |
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).