Espejos: Reflexión de la luz
Reflexión de la luz
La luz tropieza con la superficie de un cuerpo cualquiera, es difundida parcial o totalmente en todas las direcciones posibles. No ocurre lo mismo cuando la superficie del cuerpo está totalmente pulimentada. Entonces, la superficie devuelve el luminoso en una dirección única que depende de la posición rayo con respecto a está superficie: se dice que el rayo se ha reflejado, y que la superficie reflectora es un espejo. La forma sencilla de los espejos es de un plano. La naturaleza nos ofrece un ejemplo en la superficie de los lagos o de las aguas tranquilas, y el hombre, desde la épocas más remotas, ha construido espejos de metal pulimentado. Mucho más tarde se fabricaron espejos de vidrio o de cristal, que reflejaban la luz mediante una a de amalgama de estaño (estaño disuelto en el mercurio, estaño de los espejos) y solamente hace menos de un siglo se ha reemplazado el estaño por una capa delgada de plata depositada por vía química.
Es sabido que los cristales o espejos planos producen, de los objetos situados delante de ellos, imágenes semejantes a dichos objetos. Estudiando el mecanismo de formación de estas imágenes llegaron los sabios de la Antigüedad al descubrimiento de las leyes de la reflexión, que se encuentran ya formuladas, por ejemplo, en el tratado de Euclides: La Catóptrica (300 años a.C., aproximadamente).
Imágenes producidas por un espejo plano
Tracemos un círculo y diámetro en un plano horizontal y dispongamos después verticalmente un espejo no plateado a lo largo del diámetro. Tomemos después dos bujías del mismo diámetro y de la misma longitud, una de las cuales se colocará en el círculo ante un espejo, que nos dará, por reflexión, su imagen. Procuremos entonces colocar la segunda bujía de forma que se superponga a la imagen observada en el espejo, lo que se logrará después de algunos tanteos, con tanta exactitud, que será imposible distinguir la segunda de la imagen de la primera. La ilusión es tan perfecta que si se enciende la bujía situada ante el espejo, la segunda parecerá también encendida y el dedo que toca la mecha parecerá situado en la llama. (Figura 1)
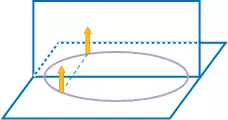
Figura 1: Imagen producida por un espejo plano
Cuando se ha obtenido esta coincidencia entre la segunda bujía y la imagen de la primera, se comprueba que la bujía número dos está también situada en el círculo, en la intersección de la perpendicular trazada desde la bujía número no sobre el diámetro. Esta disposición es sólo la simetría con respecto a un plano - el espejo - que se estudia en geometría. Se observa, además, que las distancias de las bujías al espejo son iguales, y que la imagen es también igual al objeto.
Dicho de otra forma, los rayos luminosos, después de reflejados por un espejo plano, parecen proceder de puntos del espacio situados detrás del espejo y simétricos del objeto. Un rayo luminoso trazado desde el punto a que llega al espejo M en el punto I se refleja según IR, como si viniera del punto A', sobre la perpendicular AH, tal como A'H = AH. (Figura 2)
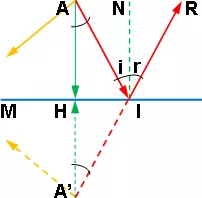
Figura 2: Diagrama de los rayos de luz que inciden y se reflejan en un espejo plano
Tracemos en la I la perpendicular IN, llamada también normal, al plano del espejo: el rayo AI se denomina rayo incidente. I es el punto de incidencia; el plano AIN, perpendicular al espejo y es que contiene a la vez el rayo y la normal, se denomina plano de incidencia, el ángulo AIN será el ángulo de incidencia î, mientras que el ángulo RIN, que forma el rayo reflejado y la normal, se denomina ángulo de reflexión r.
Primera ley de la reflexión: Los triángulos rectángulos AHI y A'HIR, que tienen un cateto común HI y los otros dos lados iguales, AH = A'H, son iguales. Los ángulos HAI y HA'I son también iguales, pero los ángulos r y HA'I por correspondientes; por consiguiente, el ángulo de incidencia es igual al ángulo de reflexión, que es la segunda ley de reflexión.
Propiedades de las imágenes producidas por los espejos planos
Los rayos reflejados por los espejos planos parecen proceder de imágenes- situadas detrás de dichos espejos: las imágenes carecen de existencia real, y se dice que son virtuales.
Consideremos ahora un rayo incidente RIA' dirigido hacia A' es detenido por el espejo en I y reflejado según IA de forma que a puede también considerarse como una imagen, esta vez real, del objeto virtual A.
El hecho que la luz pueda circular a lo largo de los rayos luminosos, en ambos sentidos, sin que se cambie de trayecto, es muy importante y constituye lo que se denomina principio del retorno inverso de la luz.
Se verá más adelante que un sistema óptico cualquiera, una imagen y su objeto son conjugados, es decir, que si se coloca un objeto. Si rayos luminosos que convergen en el mismo punto son detenidos por un espejo plano, convergerán después de reflejados, formando un verdadero punto luminoso, que es entonces una imagen real.
Las imágenes producidas por loe espejos planos tienen las mismas dimensiones que los objetos correspondientes, pero de ellos no se deduce que sean iguales. El objeto y la imagen no pueden superponerse, pero son simétricos con respecto a un plano como lo son la mano derecha y la mano izquierda; como se sabe, no es posible introducir la mano derecha en un guante izquierdo, ni inversamente. Resulta, pues, que un texto escrito o impreso no puede leerse mediante reflexión en un espejo; pero si los rayos luminosos se reflejan nuevamente en un segundo espejo, la imagen sufre una segunda inversión; así, un texto se hace legible mediante dos reflexiones.
Campo de un espejo
Un espejo no da solamente la imagen de una parte restringida del espacio situado ante él; la experiencia muestra que esta porción, visible por reflexión, denominada campo del espejo, depende a la vez de la posición del observador y de las dimensiones del espejo. En efecto, los únicos rayos incidentes que penetran en el ojo O del observador, previa reflexión, son evidentemente los dirigidos hacia O', imagen de O en el espejo. Los únicos objetos visibles en el campo del espejo son, pues, los que están situados en el interior del tronco de cono o de pirámide, de vértice O', circunscrito al espejo (Figura 3).
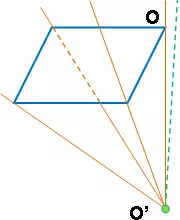
Figura 3: Campo de un espejo plano
Espejos paralelos
Consideremos que dos espejos planos M₁ y M₂ exactamente paralelos, cuyas caras reflectoras están orientadas hacia el objeto situado entre ambos. El observador situado hacia a ve un número imágenes tanto mayor cuanto más largos son los espejos. (Figura 4).
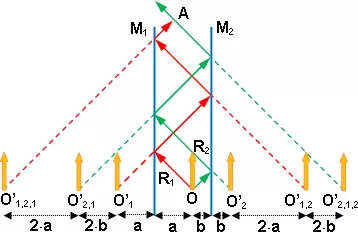
Figura 4: Diagrama de los rayos de luz que inciden y se reflejan en espejos planos y paralelos
En efecto, un rayo luminoso como el R₁ es reflejado por el espejo M₁ como si procediera de la imagen O'₁ simétrica de O con respecto al plano M₁ después encuentra el segundo espejo M₂ sobre el cual se refleja de nuevo como si procediera de la imagen O'₁ producida por M₂ es decir, de O'₁₂ en el espejo M₁ y, por consiguiente, de O'₁₂₁; una nueva reflexión puede producirse sobre M₂, etc., pero existe otra segunda serie. En efecto, un rayo como R₂ que incidiera primeramente sobre el espejo M₂ se alejaría como si procediera de la imagen O'₂₁₂ etc.
Todas estas imágenes están alineadas sobre una misma recta perpendicular a los dos lados de los espejos que pasan por O. Es fácil ver que están dispuestas alternativamente de cara y de espalda, y que las distancias entre ellas son alternativamente 2·a y 2·b si a y b son las distancias del objeto O a los espejos M₁ y M₂ respectivamente.
Cuando los dos espejos no son exactamente paralelos, las imágenes están ya alineadas sobre una misma recta, sino sobre un círculo radio más o menos grande; esta observación permite ajustar el paralelismo de los espejos.
Espejos angulares
Supongamos ahora que los espejos M₁ y M₂ sean rectangulares:
Encontraremos, como en el caso anterior, dos series de imágenes, pero en un número muy limitado, debido a que: un rayo luminoso trazado desde el objeto O no puede sufrir más que dos reflexiones, en los casos más favorables, y 2°, ciertas imágenes coinciden.
El rayo luminoso R₁ se refleja sobre M₁ (Figura 5).
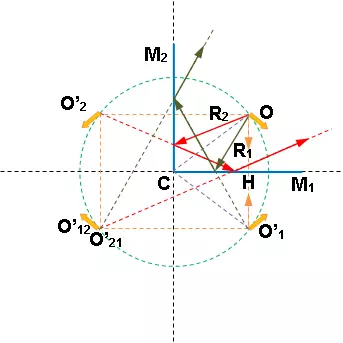
Figura 5: Espejos angulares
Como si procediera de la imagen O'₁ después de encontrar M₂ es reflejado en dirección de la imagen O'₁₂, y no puede sufrir otras reflexiones, antes de ser recibido por el observador. Un segundo rayo como el R₂ que se refleja primeramente en M₂ procedente de la imagen O'₂ cae después sobre el espejo M₁, por el que es reflejado de nuevo como si procediera de la imagen O'₂₁, simétrica de O'₂ con respecto al plano M₁. Es evidente que las imágenes O'₁₂ y O'₂₁ coincidan en posición y sentido, y que, además, las tres imágenes del objeto están situadas sobre un mismo círculo de centro C y radio CO. Si el ángulo que forman los espejos no es exactamente de 90°, las dos imágenes O'₁₂ y O'₂₁ ya coinciden; su distancia es tanto mayor cuanto más difiere de 90° el ángulo que forman los espejos. Así se tiene un procedimiento cómodo para ajustar la perpendicular de dos espejos.
Consideremos el caso en que el ángulo de los espejos es de 60°. La figura 6.
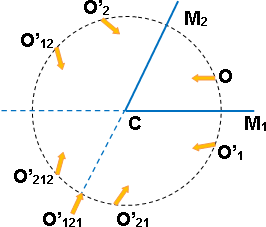
Figura 6: Imágenes generadas en espejos angulares
Muestra que se observan entonces cinco imágenes situadas en un círculo que pasa por el objeto. De una manera general, si el ángulo de los espejos es 1/n de circunferencia, el número de imágenes es n - 1. Por ejemplo, para el ángulo de 45°, que es de ⅛ de circunferencia, habrá 8 - 1 = 7 imágenes.
Caleidoscopio
Este instrumento, debido al físico inglés David Brewster (1.818), es una aplicación de los espejos angulares. En un cilindro bastante largo se introducen dos espejos, que forman entre si un ángulo de 60° Uno de los fondos del tubo cilíndrico está constituido por un vidrio de color, barbas de plumas, etc., cuyas posiciones relativas pueden variar sacudiendo el instrumento o golpeando ligeramente el tubo. El observador mira los objetos y sus imágenes a través de un agujero pequeño perforado el otro lado del tubo. Las imágenes, a causa de su simetría, forman motivos decorativos susceptibles de interesar a los dibujantes. (Figura 7)
Figura 7: Caleidoscopio
Espejo triple
Se disponen tres espejos planos, perpendiculares entre si, de forma que se constituyan un triedro trirrectángulo. En una habitación, dos paredes continuas y el suelo forman un triedro trirrectángulo).
Un rayo luminoso que incida en uno de los tres espejos sufre varias reflexiones, siendo finalmente devuelto, paralelamente a su dirección primitiva, hacia la fuente luminosa. Esta propiedad no depende de la orientación del triedro con respecto al rayo (Fig.8).
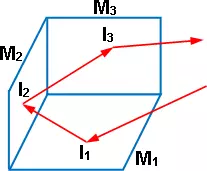
Figura 8: Incidencia de los rayos en un espejo triple
Este sistema de espejos se utiliza en las señalizaciones. Una de as estaciones está dotada de un proyector orientado hacia el espejo triple, colocado en la segunda estación. Los rayos luminosos, después de sufrir una reflexión, regresan hacia el proyector y sólo pueden ser recogidos por los vigías de la primera Estación. Los señalizadores de la segunda estación corresponden con la primera estación maniobrando ante el espejo triple una pantalla opaca con un arreglo a un código convenido; los de la primera estación pueden responder maniobrando una pantalla situada ante su proyector.
Espejo giratorio
Cuando gira un espejo plano, los rayos reflejados son desviados e imagen se desplaza; se estudiara sólo el caso más simple, que es también el más importante, el de un espejo que gira alrededor de un eje situado en un plano.
Cuando el espejo M gira del ángulo â alrededor del eje I, el rayo reflejado IR toma la dirección IR₁ obtengamos el valor del ángulo RIR₁ la normal IN en el punto de incidencia ha girado también el ángulo â y se encuentra en IN₁ el ángulo de incidencia î + NIN₁ = = î + â; con arreglo a ley de la reflexión, este valor es también el de nuevo ángulo r₁ = N₁IR₁, pero (Fig.9)
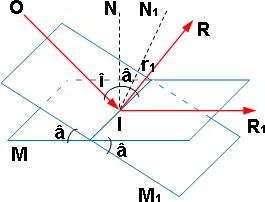
Figura 9: Incidencia de los rayos en un espejo giratorio
N₁IR₁ = NIR - NIN₁ = NIR + RIR₂- NIN
ôî + â = î + RIR₁ - â
es decir RIR₁ = 2â
Así pues, el rayo reflejado gira de un ángulo exactamente doble espejo. Más adelante se verá la aplicación de este resultado a medida del ángulos.
En cuanto a la imagen O' del objeto O es arrastrada por la rotación del espejo hacia O'₁. Como las distancias OI y O'₁I son ambas iguales a OI, resulta que la imagen O' se desplaza sobre una circunferencia de centro I y de radio IO (Figura 10).
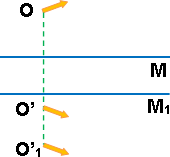
Figura 10: Espejo giratorio
Cuando se desplaza un espejo plano permaneciendo paralelo a si mismo (traslación) por ejemplo de M a M₁ muestra la figura que la del punto O que va desde O' a O'₁ se desplaza el doble: O'O₁ = 2·MM₁ (Figura 11)
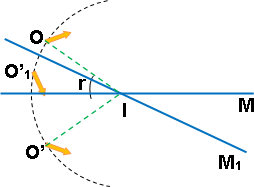
Figura 11: Espejo giratorio
Heliostatos
Entre las numerosas aplicaciones de los espejos planos pueden citarse los helióstatos. Los rayos solares muy intensos pueden utilizarse con provecho para iluminar instrumentos de física o de observación. Para ello basta con enviarlos, mediante un espejo, en la dirección escogida, pero es necesario modificar continuamente la posición de este espejo para compensar el desplazamiento del sol en horizonte, desplazamiento que varia con la hora y la latitud del lugar. Se han construido instrumentos denominados helióstatos en los cuales un mecanismo accionado por un pequeño reloj mantiene los rayos reflejados por el espejo en una dirección fija.
Bibliografía:
- VALERO, Michel. Física Fundamental. Ed. Norma
- Enciclopedia Larousse tomo 2
- FISICA, MATERIA Y ATOMOS: Círculo de lectores
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Cuáles son los instrumentos ópticos y para qué sirven?