Lentes
Dioptrio esférico
Es estudio de la refracción de un rayo luminoso a través de una superficie esférica (porción de esfera o casquete esférico) que separa dos medios refringentes diferentes es importante porque permite establecer fácilmente la teoría de los lentes.
Puede construirse un dioptrio esférico tallando una superficie esférica en el extremo de una varilla de vidrio cilíndrica. Un medio todavía más simple consiste en pegar en la extremidad de un vidrio de lámpara cilíndrica un vidrio de reloj esférico delgado.
El sistema, mantenido verticalmente, se llena de agua (Figura 1)
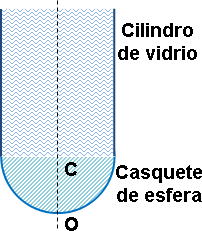
Figura 1: Esquema del dioptrio esférico
Fórmula del dioptrio
Toda recta que pase por el centro de la esfera es un eje óptico. Consideremos un punto luminoso P (Figura 2), que forme con el centro de la esfera el eje óptico PO. Demostraremos que un rayo luminoso cualquiera como el PI, siempre que forme con el eje óptico un ángulo que no exceda de algunos grados, se refracta según IP', pasando por un punto fijo P' del eje óptico. Este punto es, por consiguiente, la imagen del punto objeto P.
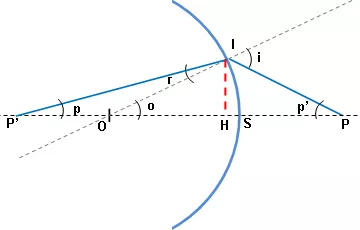
Figura 2: Incidencia de los rayos en una lente esférica
Verificación experimental
La fórmula del dioptrio puede verificarse utilizando el dispositivo el vidrio de lámpara llena de agua. El objeto será una lámpara eléctrica; se buscará la imagen utilizando un pequeño vidrio esmerilado sumergido en el agua y manteniendo en el extremo de una ranura metálica.
Se comprobará fácilmente que un pequeño objeto perpendicular al eje óptico tiene una imagen también perpendicular a este eje. Una construcción geométrica sencilla permite obtener la imagen cuando se conoce la posición de los focos F y F'. (Figura 3)
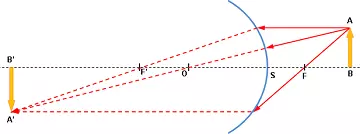
Figura 3: Formación de la imagen en una lente esférica
Un rayo procedente del punto a y paralelo al eje óptico se refracta, como si procediera de un punto infinitamente alejado, pasando por el foco F' Análogamente, un rayo incidente AF que pase por el foco-objeto, se refracta paralelamente al eje, porque la imagen de F está infinitamente alejada de S.
Esos dos rayos refractados se cortan en a, imagen el punto a, y la imagen del objeto AB es A'B. Pueden observarse que el rayo incidente AO, que pasa por el centro de la esfera, se refracta sin desviación y alcanza A'.
Lentes esféricas delgadas
Se denominan lentes sólidos de materia transparente: vidrio, cristal, cuarzo, sal gema, etc., que constan de dos caras, que son casquetes esféricos, o bien una cara plana y otra esférica. El borde de los lentes suele ser, por lo general, circular, pero puede también tener otra forma; por ejemplo, los cristales de los antiguos anteojos eran ovalados o elípticos. Se denomina eje óptico de una lente la recta que pasa por los centros O y O' de las dos esferas que limitan la cara, o la recta que pasa por el centro de la esfera perpendicular a la cara plana. Este eje atraviesa la lente en dos puntos S y S' denominados vértices. (Figura 4).
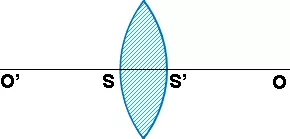
Figura 4: Esquema de una lente esférica delgada
Pueden ocurrir dos casos: o bien el espesor de la lente en el centro, es decir, la distancia SS' entre los vértices es superior al espesor del borde, en cuyo caso se dice que la lente es convergente, o bien, inversamente, el espesor en el centro SS' es menor que el borde, y entonces la lente es divergente. En cada tipo de lente se encuentran tres formas posibles, que tienen nombres particulares y que describiremos a continuación, agrupándolas en un cuadro para mayor claridad. (Figura 5).
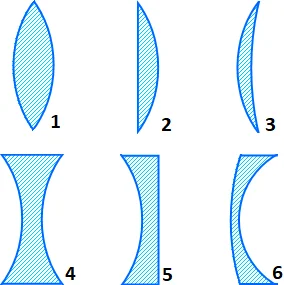
Figura 5: Tipos de lentes esféricas delgadas
1. Biconvexa; 2. Planoconvexa; 3. Menisco convergente, Bicóncava; 5. Planocóncava; 6. Menisco divergente.
Estudio experimental de las lentes convergentes
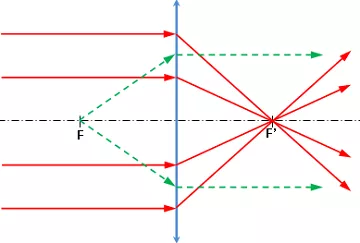
Figura 5: Incidencia de los rayos en las lentes convergentes
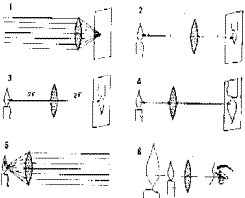
Figura 6: Formación de la imagen en la lente convergente
1) Dirijamos la lente hacia objetos muy alejados, pero bien iluminados. Sobre una pantalla de papel o cartón blanco, o sobre un vidrio esmerilado, podrá obtenerse una imagen real invertida y muy pequeña de los objetos. Los rayos luminoso que han atravesado la lente convergen en la pantalla colocada detrás de la misma, a una distancia determinada que se llama, en este caso, distancia o longitud focal (figuras. 5 y 6). El plano en el que está situada la pantalla es el plano focal, es atravesado por el eje óptico en un punto especialmente importante: el foco principal imagen (los restantes puntos del plano focal en los focos secundarios).
Si se invierten las caras de la lente (delgada), el plano focal vuelve a encontrarse a la misma distancia.
2) Aproximemos el objeto a la lente. Sea este objeto, por ejemplo, una bujía o una lámpara cualquiera. Se comprueba que es necesario alejar la pantalla para obtener una imagen neta, siempre invertida, pero mayor que la anterior. (Figura 6 [2]).
3) Cuando el objeto está situado a una distancia de la lente exactamente igual al doble de la longitud focal, hay que colocar la pantalla detrás de la lente, a una distancia también doble de la longitud focal. La imagen, que continúa siendo invertida, tiene entonces la misma dimensión que el objeto (Figura 6 [3]).
4) Continuemos aproximando el objeto a la lente; la imagen se aleja cada vez más y continúa aumentando, siempre invertida (Figura 6 [4]).
5) Cuando la distancia del objeto a la lente es igual a la longitud focal, ya no puede recogerse su imagen en la pantalla, por estar demasiado alejada: se dice que la imagen está en el infinito. Nos encontramos entonces en el caso inverso al primero. El objeto es el que ocupa el plano focal situado adelante de la lente (plano foco-objeto) y la imagen está infinitamente alejada. A este plano focal le corresponde un foco principal objeto (Figura 6 [5]).
6) Acerquemos el objeto todavía más, situándolo entre el foco y la lente: no podrá obtenerse imagen alguna sobre la pantalla, cualquiera que sea la posición de está ultima. No obstante, si nos colocamos detrás de la lente, divisaremos al mismo lado que el objeto una imagen aumentada y del mismo sentido que el objeto, es decir, una imagen virtual y derecha (Figura 6 [6]).
Lentes divergentes
Seguiremos en el estudio de estas lentes la misma marcha que en el caso de los convergentes. No es posible recoger en una pantalla la imagen de un objeto real, cualquiera que sea su posición con respecto al lente.
Es posible, no obstante, ver esta imagen 1 que parece situada al mismo lado que el objeto con respecto a la lente, y más cerca de esta última; por consiguiente, es virtual y derecha, del mismo sentido que el objeto. Existe, también, un plano focal-imagen virtual, en el que se encuentran situadas las imágenes de los puntos infinitamente alejados de la lente. Los dos focos principales equidistantes también de la lente, pero están invertidas, por hallarse el foco-objeto F a la derecha, si el sentido de la luz es de izquierda a derecha, y el foco-imagen F a la izquierda.
Defectos de las lentes
Las lentes, incluso delgadas, presentan defectos, denominados también aberraciones. Estas aberraciones pueden manifestarse de diferentes formas, según las propiedades que traten de obtenerse:
1) Si se desea obtener de un punto-objeto una imagen lo más fina posible (como sucederá con los anteojos astronómicos), habrá que corregir la aberración de esfericidad del sistema óptico. Esta aberración se manifiesta de que por el hecho que los rayos refractados por los bordes de la lente (rayos marginales) cortan el eje óptico en puntos que están más cerca de la lente que los rayos centrales. (Figura 7). Es posible suprimir está aberración con una sola lente, ya que depende del índice del vidrio, de los radios de curvatura (forma de la lente), de su orientación con respecto a la luz incidente y de la distancia del objeto. Es mínima para un objeto situado en infinito cuando el radio de la cara de entrada es seis veces menor que el de la cara de salida. En la práctica, se toma la forma planoconvexa. Para suprimir la aberración de esfericidad, hay que utilizar varios lentes.
2) Una de las aberraciones más molestas de las lentes es la aberración cromática; consideraremos una lente convergente que da en su foco la imagen de una fuente luminosa blanca muy alejada. Los bordes de la lente, actuando como prismas de ángulos pequeños (Figura 8). Desvían más los rayos rojos, de donde (Figuras 7 y 8). Desvían más los rayos rojos, de donde resulta que el foco de los rayos azules y violeta se encuentran más cerca de la lente que el foco de los rayos rojos.
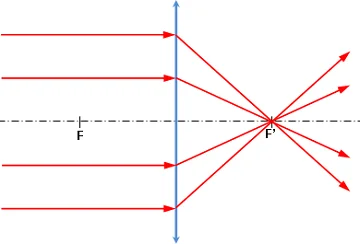
Figura 7: Aberración de esfericidad
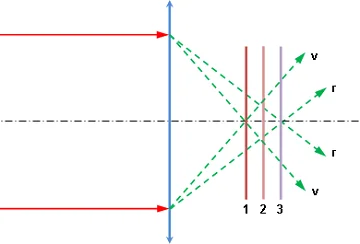
Figura 8: Aberración cromática
Si se coloca una pantalla en la posición 1, se obtendrá una mancha circular con bordes rojos. En la posición 2, la mancha tendrá un diámetro mínimo, pero sus bordes estarán todavía coloreados, produciendo la superposición del violeta y el rojo púrpura y rosa pálido. En la posición 3, aparecerá en la pantalla una mancha circula con borde violeta. La distancia entre los focos de los rayos rojos y los rayos azules es relativamente considerable, variando según la naturaleza del vidrio entre 1/60 y 1/30 de la longitud focal.
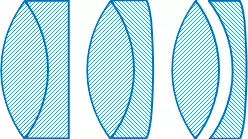
Composición de lentes acromáticas
Para corregir esta aberración y obtener lentes acromáticas, se adhieren a lentes convergentes talladas en vidrios poco dispersivos, denominados crowns, lentes divergentes de vidrios muy dispersivos, los flints, constituidos a base de silicato de plomo, como el cristal. En la figura 9 pueden verse tipos de lentes acromáticas corregidas también de la aberración de esfericidad.
3) Las otras aberraciones tiene de particular que dependen no solamente de la posición y de la abertura del diafragma que pueda acompañar a la lente. En primer lugar, la imagen de un objeto plano perpendicular al eje óptico es una superficie curva de revolución alrededor de este eje. Sobre una pantalla plana perpendicular al eje se recibe la imagen de un cuadrado, puedo obtenerse una figura cuyos lados son más o menos abombados en forma de la media luna, o bien en forma de tonel (figura 10), esta aberración se llama distorsión, y es debida a que el aumento lineal varia al alejarse del eje.
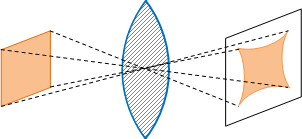
Figura 9: Lentes acromáticas | 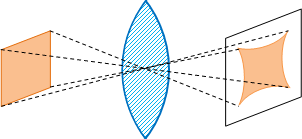
Figura 10: Aberración de distorsión |
Señalaremos, finalmente, la última aberración: el astigmatismo, que se manifiesta principalmente si se toma como objeto un plano en el que han trazado círculos centrados en el eje y radios salidos del centro. Es imposible ajustar en una pantalla plana (figuras 11 y 12), círculos y radios al mismo tiempo.
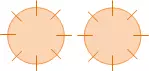
Figura 11: Aberración de astigmatismo | 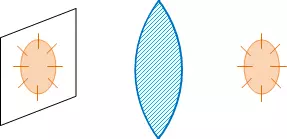
Figura 12: Corrección del astigmatismo |
Se logra corregir más o menos todas estas aberraciones utilizando varios lentes de vidrios diferentes adheridas o separados por intervalos de aire, y disponiendo el diafragma convenientemente, ya delante, detrás o entre los lentes.
Bibliografía:
- VALERO, Michel. Física Fundamental. Ed. Norma
- Enciclopedia Larousse tomo 2
- FISICA, MATERIA Y ATOMOS: Círculo de lectores
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es un lente divergente? Ejemplos. ¿Cuáles son los diferentes tipos de lentes?