Problema nº 4 de variación de la longitud ocasionada por la dilatación - TP01

Enunciado del ejercicio nº 4

Calcular la relación de longitudes que deben cumplir dos varillas cuyos coeficientes de dilatación son de 0,0000097/°C y 0,0000117/°C, para que a cualquier temperatura la diferencia sea de 5 cm.

Desarrollo

Datos:

Diferencia = 5 cm = 0,05 m

αᵥ₁ = 0,0000097/°C

αᵥ₂ = 0,0000117/°C

Fórmulas:

Δl = α·l₁·Δt°

Esquema:

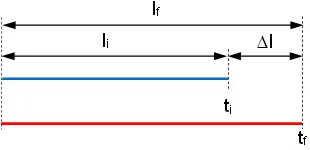
Solución

Δlᵥ₁ = αᵥ₁·lᵥ₁·Δt°ᵥ₁

Δlᵥ₂ = αᵥ₂·lᵥ₂·Δt°ᵥ₂

Las temperaturas iniciales y finales son iguales:

Δt°ᵥ₁ = Δt°ᵥ₂

Lo que pide es:

Δlᵥ₁ - Δlᵥ₂ = 0,05 m

Pero esto no es opción, porque depende de los coeficientes de dilatación de cada metal y se resuelve haciendo la razón entre ellos:

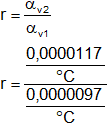
Cálculo de la dilatación lineal

r = 1,206185567

Resultado, la relación de longitudes entre las varillas es:

r = 1,2062

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la variación de longitud ocasionada por la dilatación. ¿Cómo calculo la dilatación lineal de una varilla?