Problema nº 8 de trabajo y potencia, energía cinética y potencial - TP05
Enunciado del ejercicio nº 8
Una partícula se desliza libremente en una pista sin rozamiento, partiendo del punto A con una determinada velocidad inicial. El plano horizontal de referencia para medir la energía potencial gravitatoria pasa por el punto B. Se sabe que la energía potencial en el punto A vale 64 J y la energía cinética en el punto B vale 128 J.
Cuando la partícula pasa por el punto C sus energías cinética y potencial respectivamente son iguales a:
a) 96 J y 32 J
b) 32 J y 32 J
c) 64 J y 64 J
d) 32 J y 96 J
e) 96 J y 96 J
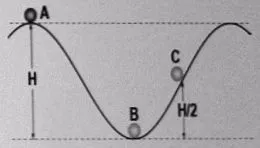
Esquema del movimiento
Desarrollo
Datos:
VA ≠ 0
EpA = 64 J
EcB = 128 J
Fórmulas:
ΔEM = ΔEc + ΔEₚ
Eₚ = m·g·h
Solución
Para el recorrido ABC tenemos que no hay rozamiento y la fuerza peso es conservativa, por lo tanto:
ΔEM = 0
Como la altura del punto C es la mitad de la altura del punto A, tendremos en el punto C (por definición de energía potencial) la mitad de la energía potencial de A:
Eₚ = m·g·h
EpA = m·g·h
EpC = ½·m·g·h = ½·EpA = ½·64 J = 32 J
EpC = 32 J
Aplicamos el teorema de la energía mecánica para el tramo BC:
0 = ΔEc + ΔEₚ
ΔEc = -ΔEₚ
EcC - EcB = EpB - EpC
La energía potencial en el punto B vale 0 porque es el nivel de referencia.
EcC - EcB = 0 - EpC
EcC - EcB = -EpC
Despejamos la energía cinática en C (será la energía que utilizará la partícula para ascender hasta el punto C):
EcC = EcB - EpC
Reemplazamos por los datos y calculamos:
EcC = 128 J - 32 J
EcC = 96 J
La respuesta correcta es (a).
Enviado por: Carlos Quipildor
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular la energía cinética y potencial