Problema nº 9 de movimiento relativo, velocidad o rapidez relativa - TP08

Enunciado del ejercicio nº 9

En un día de verano en que no hay viento se descarga un chaparrón, de modo tal que las gotas de agua siguen trayectorias verticales. El conductor de un auto que marcha a 10 km/h ve que las gotas llegan en dirección vertical al parabrisas. Sabiendo que el parabrisas forma un ángulo de 60° con la horizontal, determinar:

a) La velocidad con que descienden las gotas de lluvia vistas desde tierra.

b) La velocidad con que golpean al parabrisas.

Desarrollo

Datos:

v_auto = 10 km/h

α = 60°

Fórmulas:

Teorema de Pitágoras

h² = a² + b²

Esquema:

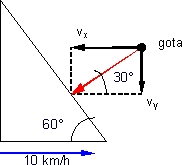
Esquema del movimiento relativo

Solución

Si el conductor ve que las gotas golpean en forma vertical (perpendicular) al prabrisas y éste tiene una inclinación de 60°, significa que las gotas tienen una inclinación de 30° con la horizontal.

a)

Aplicando trigonometría:

tg α = v_y/v_auto

v_auto·tg α = v_y

v_y = (10 km/h)·tg 30°

Resultado, velocidad con que descienden las gotas de lluvia es:

v_y = 5,77 km/h

b)

Luego, aplicando el Teorema de Pitágoras:

Reemplazamos por los datos y resolvemos:

Resultado, velocidad con que las gotas golpean al parabrisas es:

v_gota = 11,55 km/h

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP08
• | Siguiente ›

Ejemplo, cómo calcular la velocidad o rapidez relativa. Nivel medio, secundaria, bachillerato, ESO.