Problema nº 1 de tiro o lanzamiento vertical, velocidades inicial y final - TP11

Enunciado del ejercicio nº 1

Se lanza un cuerpo verticalmente hacia abajo con una velocidad inicial de 7 m/s.

a) ¿Cuál será su velocidad luego de haber descendido 3 s?

b) ¿Qué distancia habrá descendido en esos 3 s?

c) ¿Cuál será su velocidad después de haber descendido 14 m?

d) Si el cuerpo se lanzó desde una altura de 200 m, ¿en cuánto tiempo alcanzará el suelo?

e) ¿Con qué velocidad lo hará?

Usar g = 10 m/s²

Desarrollo

Datos:

v₀ = 7 m/s

t = 3 s

y = 200 m

h = 14 m

Fórmulas:

v_f = v₀ + g·t (1)

y = v₀·t + ½·g·t² (2)

v_f² - v₀² = 2·g·h (3)

Solución

De la ecuación (1):

v_f = (7 m/s) + (10 m/s²)·(3 s)

Resultado, la velocidad luego de haber descendido 3 s es:

v_f = 37 m/s

De la ecuación (2):

Δh = (7 m/s)·(3 s) + ½·(10 m/s²)·(3 s)²

Resultado, la distancia luego de haber descendido 3 s es:

Δh = 66 m

De la ecuación (3):

v_f = √v₀² + 2·g·h

Resultado, la velocidad luego de haber descendido 14 m es:

v_f = 18,14 m/s

De la ecuación (2):

0 = v₀·t + ½·g·t² - y

Aplicamos la ecuación cuadrática (Báscara o Bhaskara) que dará dos resultados:

t_1,2 =	-v₀ ± √v₀² - 4·½·g·(-y)
	2·½·g

t_1,2 =	-v₀ ± √v₀² + 2·g·y
	g

t₁ =	-v₀ + √v₀² + 2·g·y
	g

t₂ =	-v₀ - √v₀² + 2·g·y
	g

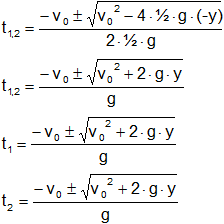
Resultado, el tiempo para alcanzar el suelo es:

t₁ = 5,66 s

t₂ = -7,06 s (No es solución)

De la ecuación (3):

v_f = √v₀² + 2·g·h

Resultado, la velocidad al tocar el suelo es:

v_f = 63,63 m/s

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular las velocidades inicial y final, con qué velocidad llega al suelo. Lanzamiento vertical en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.