Problema nº 2 de tiro o lanzamiento vertical, lanzamiento vertical - TP11
Enunciado del ejercicio nº 2
Se lanza un cuerpo verticalmente hacia arriba con una velocidad inicial de 100 m/s, luego de 4 s de efectuado el lanzamiento su velocidad es de 60 m/s.
a) ¿Cuál es la altura máxima alcanzada?
b) ¿En qué tiempo recorre el móvil esa distancia?
c) ¿Cuánto tarda en volver al punto de partida desde que se lo lanzo?
d) ¿Cuánto tarda en alcanzar alturas de 300 m y 600 m?
Usar g = 10 m/s²
Desarrollo
Datos:
v₀ = 100 m/s
vf = 60 m/s
t = 4 s
y₁ = 300 m
y₂ = 600 m
Fórmulas:
vf = v₀ + g·t (1)
y = v₀·t + ½·g·t² (2)
vf² - v₀² = 2·g·h (3)
Esquema:
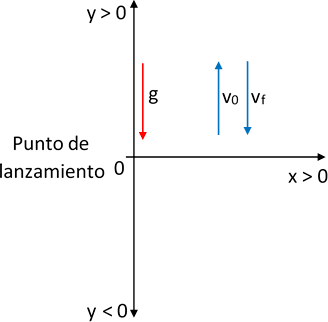
Sentido de los vectores en el tiro vertical hacia arriba
Solución
a)
Para la altura máxima vf = 0, de la ecuación (3):
-v₀² = 2·g·h
![]()
Reemplazamos por los valores y calculamos:
![]()
Resultado, la altura máxima alcanzada es:
hₘₐₓ = 500 m
b)
De la ecuación (1) y para vf = 0:
![]()
Reemplazamos por los valores y calculamos:
![]()
Resultado, el tiempo que tarda en recorrer la distancia es:
t = 10 s
c)
Recordemos que en tiro vertical, cuando un objeto es lanzado hacia arriba y luego cae, cuando vuelve a pasar por el punto de partida posee la misma velocidad que en el momento del lanzamiento pero con sentido contrario (vf = -v₀).
Podemos asegurar que el resultado pedido es el doble del tiempo que requirió para alcanzar la altura máxima.
Resultado, el tiempo que tarda en volver al punto de partida desde que se lanzó es:
t = 20 s
d)
No puede alcanzar una altura de 600 m porque la máxima es de 500 m. Para h = 300 m empleamos la ecuación (2):
0 = v₀·t + ½·g·t² - y
Aplicamos la ecuación cuadrática (Báscara o Bhaskara) que dará dos resultados:
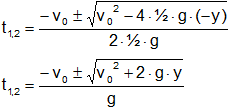
Reemplazamos por los valores y calculamos:
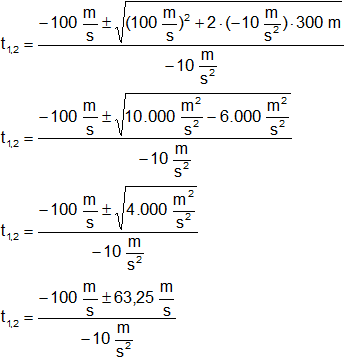
Separamos las ecuaciones una por cada signo y resolvemos:
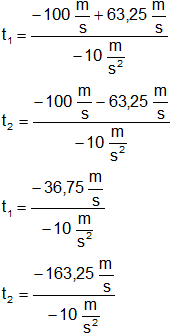
t₁ = 3,67 s
t₂ = 16,32 s
Resultado, el tiempo que tarda en alcanzar la altura de 300 m es:
t₁ = 3,67 s
t₂ = 16,32 s (No es solución)
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP11
- | Siguiente ›
Ejemplo, cómo calcular el tiempo que demora en alcanzar distintas alturas. Lanzamiento vertical en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.