Problema nº 1 de movimiento circular en el plano, velocidad tangencial y velocidad angular - TP18

Enunciado del ejercicio nº 1

a) ¿Cuál es la velocidad angular de un punto dotado de M.C.U. si su período es de 1,4 s?

b) ¿Cuál es la velocidad tangencial si el radio es de 80 cm?

Desarrollo

Datos:

T = 1,4 s

r = 80 cm = 0,80 m

Fórmulas:

(1)

(2)

Solución

a)

Aplicamos la ecuación (1) para hallar la velocidad angular:

Reemplazamos por los datos y calculamos:

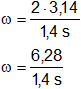
Resultado, la velocidad angular es:

ω = 4,488 s⁻¹

b)

Para hallar la velocidad tangencial empleamos la ecuación (2):

Reemplazamos por los datos y calculamos:

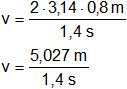
Resultado, la velocidad tangencial es:

v = 3,59 m/s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP18
• | Siguiente ›

Ejemplo, cómo calcular la velocidad tangencial y la velocidad angular en el movimiento circular uniforme. Nivel medio, secundaria, bachillerato, ESO.