Problema nº 2 de movimiento circular en el plano, período y velocidad angular - TP18
Enunciado del ejercicio nº 2
Si un motor cumple 8.000 RPM, determinar:
a) ¿Cuál es su velocidad angular?
b) ¿Cuál es su período?
Desarrollo
Datos:
f = 8.000 RPM
Fórmulas:
![]() (1)
(1)
Solución
a)
Convertimos las RPM en frecuencia angular ω:
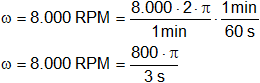
Resultado, la velocidad angular es:
ω = 837,76 s⁻¹
b)
Para hallar el período empleamos la ecuación (1):
![]()
Despejamos T:
![]()
Reemplazamos por los datos y calculamos:
![]()
Resultado, el período es:
T = 0,0075 s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP18
- | Siguiente ›
Ejemplo, cómo calcular el período y la velocidad angular en el movimiento circular uniforme. Nivel medio, secundaria, bachillerato, ESO.