Problema nº 1 de encuentro, lugar y tiempo de encuentro - TP20

Enunciado del ejercicio nº 1

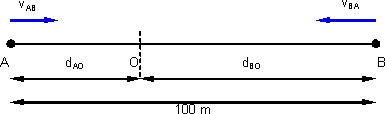
Dos puntos "a" y "b" están separados por una distancia de 100 m. En un mismo momento pasan dos móviles, uno desde "a" hacia "b" y el otro desde "b" hacia "a", con MRU, de tal manera que uno de ellos tarda 2 s en llegar al punto "b" y el otro 1,5 s en llegar al punto "a". Hallar:

a) El punto de encuentro.

b) El instante del encuentro.

Desarrollo

Datos:

d_AB = 100 m

t_AB = 2 s

t_BA = 1,5 s

Fórmulas:

(1)

(2)

El gráfico es:

Solución

a)

Para el punto de encuentro:

d_AB = d_AO + d_BO (3)

Siendo el punto O el punto de encuentro.

Como ambos comienzan su movimiento en el mismo instante el tiempo de encuentro es el mismo para ambos móviles.

t_AO = t_BO = t_E

Para el encuentro las (1) y (2) ecuaciones quedan:

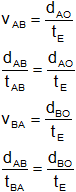
Despejamos (t_E) y luego igualamos:

(4)

(5)

t_AB·d_AO = t_BA·d_BO

De la ecuación (3):

d_AO = d_AB - d_BO

t_AB·(d_AB - d_BO) = t_BA·d_BO

t_AB·d_AB - t_AB·d_BO = t_BA·d_BO

t_AB·d_AB = t_AB·d_BO + t_BA·d_BO

t_AB·d_AB = (t_AB + t_BA)·d_BO

Reemplazamos por los valores y calculamos:

Resultado, el punto de encuentro es:

d_BO = 57,14 m (desde el punto B)

ó

d_AO = 42,86 m (desde el punto A)

b)

Empleando la ecuación (4) ó (5):

Resultado, el momento del encuentro es:

t_E = 0,86 s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP20
• | Siguiente ›

Ejemplo, cómo calcular el lugar y tiempo de encuentro en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.