Problema n° 6 de fuerza peso, masa y gravedad - TP01

Enunciado del ejercicio n° 6

Si al tirar de una masa m₁, ésta experimenta una aceleración a, ¿cuál debe ser la masa m₂ que se agrega, como indica la figura, para que tirando con la misma fuerza, la aceleración que logre el sistema sea a/2?

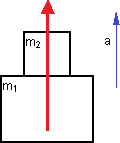
Esquema de los cuerpos y la fuerza

Desarrollo

Datos:

a = a_A

a_B = ½·a_A

Fórmulas:

F = m·a

P = m·g

Condición de equilibrio (Primera ley de Newton):

∑F_x = 0

∑F_y = 0

∑MF = 0

Solución

Condición de equilibrio:

∑F = 0

Si hay movimiento:

∑F = m·a

La situación inicial es:

F - m₁·g = m·a_A (1)

Y el enunciado propone:

F - m₁·g - m₂·g = m·a_B (2)

El enunciado establece que:

a_B = ½·a_A (3)

Por lo tanto, reemplazando (3) en la ecuación (2) queda:

F - m₁·g - m₂·g = m·½·a_A (4)

Sabemos que m es la masa total del sistema donde se aplica la fuerza resultante:

m = m₁ + m₂ (5)

Formando un sistema de ecuaciones:

F - m₁·g = m·a_A (1)

F - m₁·g - m₂·g = m·½·a_A (4)

Aplicamos el método se sustracción para resolver ecuaciones haciendo (1) - (4):

F	- m₁·g		=	m·a_A
- F	+ m₁·g	+ m₂·g	=	- ½·m·a_A
0	0	m₂·g	=	½·m·a_A

m₂·g = ½·m·a_A (6)

Reemplazamos (5) en (6)

m₂·g = ½·(m₁ + m₂)·a_A

Resolvemos:

m₂·g = ½·(m₁ + m₂)·a_A

2·m₂·g = (m₁ + m₂)·a_A

2·m₂·g = m₁·a_A + m₂·a_A

2·m₂·g - m₂·a_A = m₁·a_A

m₂·(2·g - a_A) = m₁·a_A

Despejamos la masa 2:

m₂ =	m₁·a_A
	2·g - a_A

Resultado, la masa adicional será:

m₂ =	m₁·a
	2·g - a

Autor: Ricardo Santiago Netto. Argentina