Problema nº 4 de dinámica con rozamiento, fuerza resultante de un sistema de masas en movimiento - TP03
Enunciado del ejercicio nº 4
La cuerda se rompe para una tensión de 1.000 N. Calcular la fuerza con la que hay que tirar de m₁ para que se rompa la cuerda, si μ = 0,1 entre los dos cuerpos, y μ = 0,2 entre m₁ y la superficie.
Desarrollo
Datos:
m₁ = 10 kg
m₂ = 1 kg
μ₁₂ = 0,1
μ₁ₛ = 0,2
T = 1.000 N
g = 10 m/s²
Fórmulas:
Fᵣ = μ·N (1)
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
Esquema:
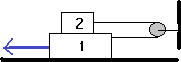
Solución
La fuerza de rozamiento siempre es contraria al movimiento y, por lo tanto, actúa como freno.
Realizamos el esquema de las fuerzas para ambas masas y planteamos las ecuaciones de equilibrio, el sentido del eje de las X será el del movimiento:
Masa "1":
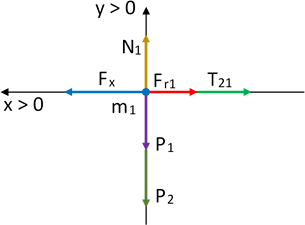
Diagrama de fuerzas para la masa 1
En el eje X:
Fₓ - Fᵣ₁ - T₂₁ = 0 (2)
Fₓ: es la fuerza mínima para vencer el rozamiento y poner al sistema en movimiento.
En el eje Y:
N₁ - P₁ - P₂ = 0 (3)
Masa "2":
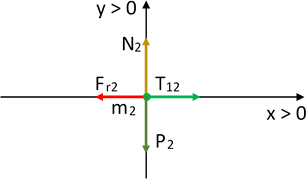
Diagrama de fuerzas para la masa 2
En el eje X:
T₁₂ - Fᵣ₂ = 0 (4)
En el eje Y:
N₂ - P₂ = 0 (5)
Planteamos todo en un mismo eje sabiendo que:
T₂₁ = T₁₂ = T
En el eje X las ecuaciones (2) y (4) quedan:
Fₓ - Fᵣ₁ - T = 0 (2)
T - Fᵣ₂ = 0 (4)
Despejamos T:
Fₓ - Fᵣ₁ = T
T = Fᵣ₂
Igualamos:
Fₓ - Fᵣ₁ = Fᵣ₂
Fₓ = Fᵣ₁ + Fᵣ₂ (6)
Respecto a las fuerzas de rozamiento empleamos la ecuación (1):
Fᵣ₁ = μ₁ₛ·N₁
Fᵣ₁ = μ₁ₛ·(P₁ + P₂)
Fᵣ₁ = μ₁ₛ·(m₁·g + m₂·g)
Fᵣ₂ = μ₁₂·N₂
Fᵣ₂ = μ₁₂·P₂
Fᵣ₂ = μ₁₂·m₂·g
Reemplazamos las fuerzas de rozamiento en la ecuación (6):
Fₓ = μ₁ₛ·(m₁·g + m₂·g) + μ₁₂·m₂·g
Reemplazamos por los valores y calculamos:
Fₓ = 0,2·(10 kg·10 m/s² + 1 kg·10 m/s²) + 0,1·1 kg·10 m/s²
Fₓ = 0,2·(100 N + 10 N) + 0,1·10 N
Fₓ = 0,2·110 N + 1 N
Fₓ = 22 N + 1 N
Fₓ = 23 N (fuerza necesaria para sacar al sistema de equilibrio)
Para romper la cuerda necesitamos sumarle a Fₓ la tensión de rotura T:
F = Fₓ + T
F = 23 N + 1.000 N
Resultado, la fuerza con la que hay que tirar de m₁ para que se rompa la cuerda es:
F = 1.023 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la fuerza resultante de un sistema de masas en movimiento