Problema nº 2 de dinámica, cuerpos sometidos a fuerzas, aceleración y sentido del movimiento
Enunciado del ejercicio nº 2
Si la tensión en el cable de un ascensor es de 2.800 N, el peso del ascensor es de 300 kgf y transporta a una persona de 80 kgf de peso. Calcular:
a) ¿Qué aceleración tiene?
b) ¿El ascensor sube o baja?
Desarrollo
Datos:
T = 2.800 N
PA = 300 kgf
PP = 80 kgf
Se adopta g = 9,80665 m/s² para pasar las unidades de kgf a N, para los cálculos posteriores g = 10 m/s²
Fórmulas:
F = m·a
P = m·g
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
Esquema:
Diagrama del cuerpo libre
Solución
Convertimos las unidades de peso:
PA = 2.942 N
PP = 784,5 N
a)
La condición de equilibrio es:
∑F = 0
Pero como hay movimiento:
∑F = m·a
La masa es:
Reemplazamos por los valores y calculamos:
m = 372,65 kg
Las fuerzas sobre el eje (tomando el eje positivo hacia arriba) son:
T - PA - PP = m·a
Reemplazamos por los valores y calculamos:
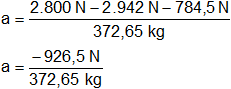
Resultado, la aceleración del ascensor es:
a = -2,49 m/s²
b)
Resultado, como la aceleración del sistema es negativa el ascensor desciende.
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo de cuerpos sometidos a fuerzas, como calcular la aceleración y el sentido del movimiento