Problema nº 5 de elasticidad en los sólidos, carga máxima, módulo de Young y estrechamiento - TP01
Enunciado del ejercicio nº 5
a) ¿Cuál es la carga máxima que puede soportar un alambre de aluminio de 0,1 cm de diámetro sin sobrepasar el límite de proporcionalidad de 8·10⁷ Pa?
b) Si el alambre tenía inicialmente 5 m de longitud, ¿cuánto se alargará bajo la acción de esta carga?
c) ¿Cuánto varía el diámetro bajo la acción de esa carga?
Desarrollo
Datos:
d = 0,1 cm
σ = 8·10⁷ Pa
l = 5 m
E = 0,7·10¹¹ Pa (Módulo de Young para el aluminio) *
ν = 0,16 (Coefisiente de Poisson para el aluminio) *
(*) Datos de la tabla de constantes de elasticidad de metales
Fórmulas:
![]()
s = π·(½·d)²
![]()
![]()
![]()
Solución
a)
Aplicamos la fórmula del módulo de Young:
![]()
Despejamos F:
F = σ·s
Convertimos las unidades de longitud:
![]()
d = 0,001 m
Calculamos la superficie de la sección transversal:
s = π·(½·d)²
s = 3,1415·(½·0,001 m)²
s = 7,85398·10⁻⁷ m²
Reemplazamos y calculamos la fuerza:
F = 8·10⁷ Pa·7,85398·10⁻⁷ m²
F = 8·7,85398·10(7 - 7) Pa·m²
F = 62,832·10⁰ N
F = 62,832 N
Resultado a), la carga máxima que puede soportar un alambre de aluminio es:
F = 62,832 N
b)
Aplicamos la fórmula de la deformación unitaria
![]()
y
![]()
Igualamos:
![]()
Despejamos Δl:
![]()
Reemplazamos por los datos y calculamos:
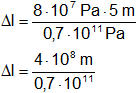
Δl = 5,714·10⁻³ m
Resultado b), el alargará bajo la acción de la carga es:
Δl = 5,714·10⁻³ m
c)
d₀ = d = 0,001 m
Aplicamos la fórmula de la variación del diámetro en función del coeficiente de Poisson:
![]()
Despejamos Δd:
![]()
Reemplazamos por los datos y calculamos:
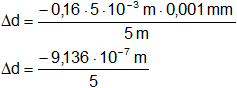
Δd = -1,829·10⁻⁷ m
Resultado c), la variación del diámetro bajo la acción de la carga es:
Δd = -1,829·10⁻⁷ m = 0,000183 mm
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo calcular la carga máxima que puede soportar un alambre